Such an electrical field oscillates from grain to
g
grain in the ice bulk following grain configurations
and is very significant even in non-doped ice grown
from distilled water, E = 100 1000 V/m. In doped ice
E can locally be as large as 104 V/m (Petrenko 1992a,
1994b).
When an ice mass is split by a crack rapidly grow-
n
ing in the direction perpendicular to the electrical field,
the field generates two surface charges of the opposite
sign λs on the opposite surfaces of the crack
λs = ε0 (εs - 1)E⊥
(33)
E
where E⊥ is a component of the electrical field perpen-
dicular to the crack surface. Inside the crack the same
ϕ
component, E⊥r , exceeds E⊥ by two orders of magni-
c
tude
E⊥r = εs E⊥
(34)
c
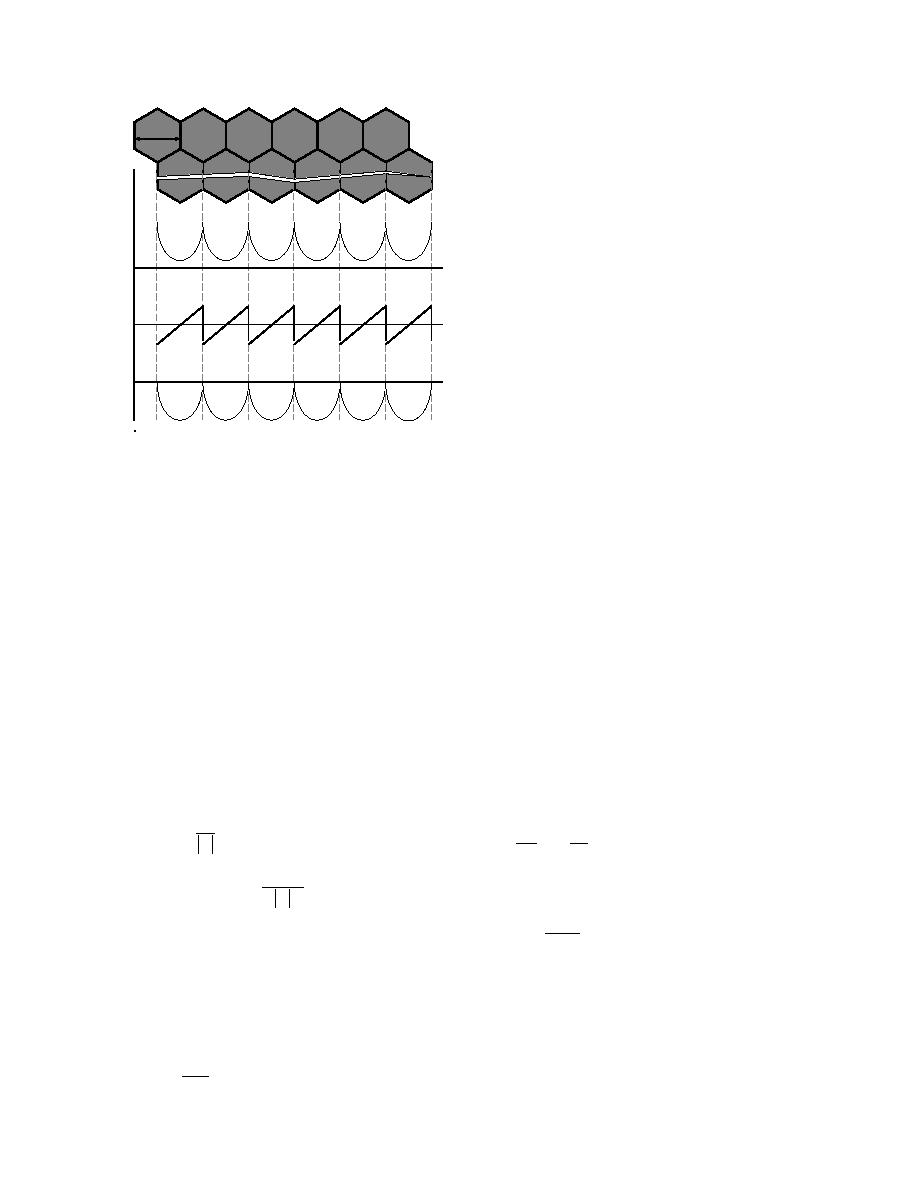
Figure 17. Schematical representation of variations
in ions' concentration n, electric field strength E and
since εs ≈ 102. Taking E⊥ = 102103 V/m, we obtain a
electric potential ϕ along the crack surface in granu-
potential difference ∆ϕ across a 1-mm wide crack
lar ice.
∆ϕ ≈ 10 100 V.
distribution of impurities in ice. Namely, when ice
(35)
grains grow, impurities are pushed out by the phase
boundary from grain centers to their peripheries, so
Such a large potential difference can easily explain
that more impurities get trapped near grain boundaries.
why the intrinsic electrical field dominates among the
This process is common for most materials and is as-
causes of EME from cracks in ice.
cribable to lower solubility of foreign atoms and ions
The processes of dielectric relaxation causes the
in a solid phase as compared with a liquid phase. Mo-
density of crack surface charges to decay with time. In
bile ions trapped in the ice bulk then diffuse against the
the case of a growing crack, this density, thus, decreas-
gradient of their concentration, generating electrical
es as the distance from the crack tip increases. Hence,
charge transport and an intrinsic electrical field in ice.
eq 3335 are applicable only in a crack tip's vicinity.
To calculate λs far from the tip, we should take into
celed with a drift flux of the ions jDR
account two processes of relaxation of electrical
charges in ice (Jaccard 1964, Gluschenkov and Petren-
jDR + jD = 0
(29)
ko 1993, Petrenko 1993a). In the first relaxation pro-
cess, λs decays exponentially with time from its initial
value λs to
where
ei
jDR =
ini E
ε∞
(30)
1
λs ≈
λs .
ei
εs
30
i kBT
jD = - Di∇ni = -
∇ni
(31)
The relaxation time of this fast process is
ei
ε∞ε0
where i =
τ1 ≈
ion mobility
.
(36)
σ∞
Di =
ion diffusion coefficient
ni =
ion concentration
At T = 10C in pure ice, τ1 ≈ 106 seconds and is
ei =
ion electric charge.
even shorter in natural ice. Since the crack velocity in
freshwater ice varies in the range from 102 to 103 m/s
Equalizing the right-hand sides of eq 30 and 31, we
find the intrinsic electrical field
(Petrenko 1992a, Sato and Wakahama 1992), the
length of a high-density surface charge train behind a
crack tip is about 106 s (102103) m/s = 0.11 mm.
∇ ln(ni ).
kBT
E=
(32)
ei
14



 Previous Page
Previous Page
