pseudo-piezoelectric effect. Indeed, that method was
used (Evtushenko and Petrenko 1991) to determine γai.
charge carriers in ice have no time to get redistributed
By varying temperature and doping, we determined
in the bulk of the deformed ice and, in the first approx-
activation volumes of all four types of protonic defects
At the lower frequencies ω = ≤ ωD, we have to allow
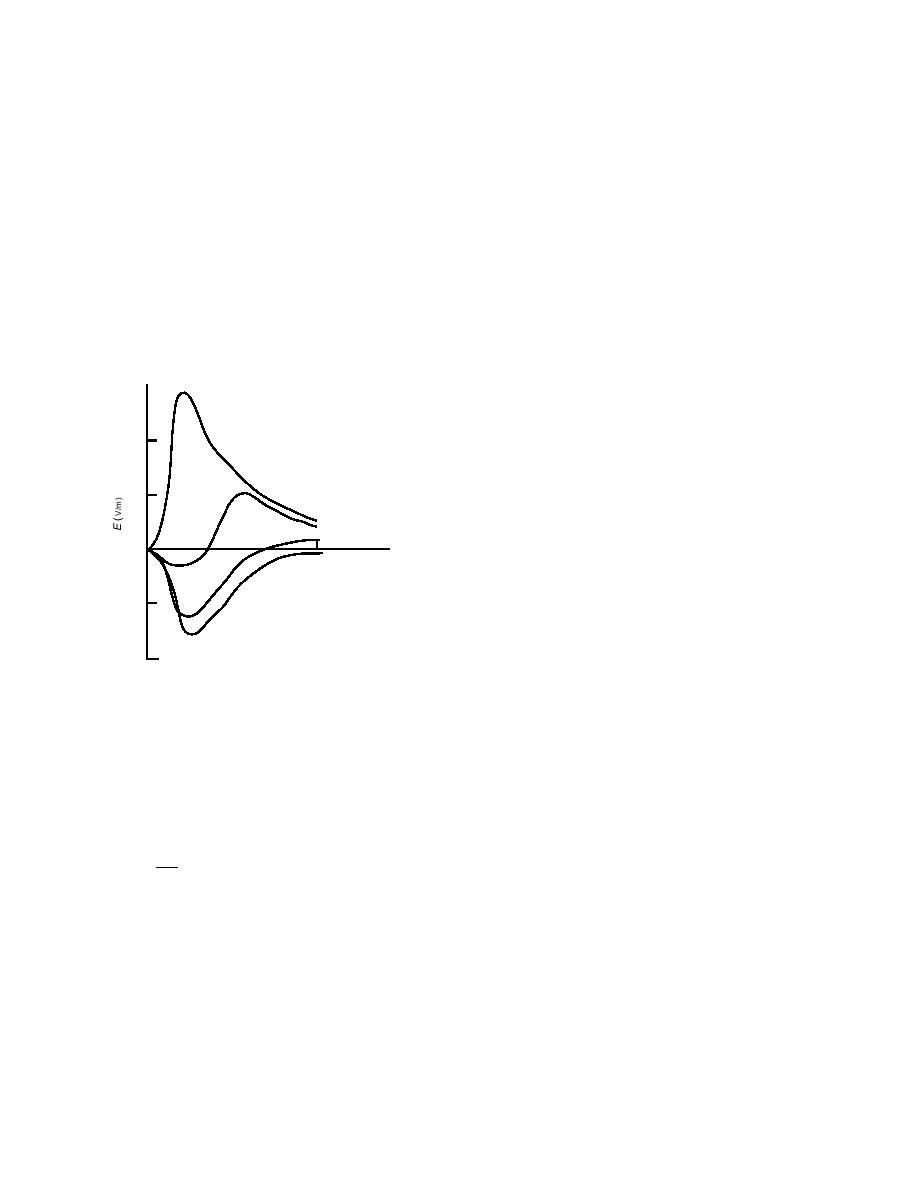
in ice. Figure 16 shows time dependencies of an elec-
trical bias generated across a thin ice sample when a
for the ac bias arising at the elastic oscillations being
step-shaped pulse of bending was applied to the sam-
applied to the bulk of ice, whose electrical conductivi-
ple. The ice was doped with NH3 in such concentration
ty and dielectric permittivity have a complicated fre-
that D-defects were majority charge carriers above
quency dependence (Hobbs 1974, Petrenko 1993b).
30C, but below 35C OH ions dominated. The ob-
Such electrical polarization induced by elastic strain in
served decay of the signals is mainly attributable to a
ice with temperature or impurity gradients, or both,
final input impedance of the measuring circuit used.
was reported by Evtushenko et al. (1987).
Since the electrical charges of OH ions and D-defects
are opposite, so are the electrical biases caused by their
ELECTROMAGNETIC PHENOMENA
migration.
IN ICE FRACTURE
At present we know of several electromagnetic
phenomena that are associated with the presence or
1. 20C.
appearance of cracks in ice. They are electromagnetic
0.1
2. 30C.
1
emissions (EME) from growing cracks and stable
3. 40C.
4. 50C.
cracks under varying stress, and also crack-induced
2
changes in electrical conductivity and apparent dielec-
tric permittivity of ice.
The most interesting and intriguing of these phen-
10
omena, EME from cracks, was primarily found under
0
t (ms)
poorly controlled field conditions when a low signal-
3
to-noise ratio left doubts and uncertainty about the
Figure 16. Oscillograms of
phenomenon's existence. Later, EME from cracks in
4
the electric field strength E
ice were reproduced and studied in a well-controlled
in the ice sample doped with
laboratory environment. The laboratory results made it
104 mole/L NH3.
possible to develop physical models that explained that
0.1
electromechanical effect. When the researchers were
equipped with these models, they succeeded in obtain-
Other pseudo-piezoelectric effects
ing reliable and well-reproducible detection of EME
There are more trivial pseudo-piezoelectric effects.
from cracking in lake and sea ice. At the present time,
They can be observed when ice is already electrically
the EMP described below in this section are well un-
polarized for some reason. For example, because of the
derstood and have even been found useful, both in ice
thermoelectric effect (Brook 1958), ice is always po-
mechanics and remote sensing of stress in ice. That is
larized when there is a temperature gradient in it. The
why we first start with a theoretical consideration of
electrical potential difference generated is usually
the physical processes that cause EME from cracks in
small since the thermoelectrical power of ice is low
ice and other associated phenomena. Then, we will
∆V
discuss laboratory and field data and their interpreta-
= (2 - 4)mV/C
(28)
tions.
∆T
Theory
(see Bryant and Fletcher 1965, Takahashi 1966). More
Cracks splitting pre-polarized ice
pronounced electrical polarization of ice can be in-
duced by nonuniform distribution of impurity ions in
The main cause of EME from cracks in natural ice is
ice. In this case ∆V can reach hundreds of millivolts
the so-called "frozen-in" or "intrinsic" electrical field
and even 1 V (Brook 1958, Petrenko 1992a). Hence,
that is always presents in both sea and freshwater ice.
we can say that a piece of ice acquires an electrical
This electrical field is generated by spatial nonunifor-
polarization if there are either temperature or impurity
mity in the concentration of ions dissolved in the ice
gradients in it. Elastic strain εij (even uniform) changes
bulk (Petrenko 1992a, 1994b). Figure 17 shows sche-
the dimensions of the ice sample, changing its dipole
matically such an electrical field inside granular ice.
moment. When a characteristic frequency of applied
The electrical field originates from the nonuniform
13




 Previous Page
Previous Page
