ELECTRO-ELASTIC EFFECTS
stress tensor in eq 14 should be of the order of P
Is ordinary ice Ih piezoelectric?
eijk ≈ P ≈ 2 1010 C/m2 .
(19)
Perhaps the most well-known electromechanical
phenomenon is piezoelectricity. Application of uni-
The reader can check that eq 19 gives the correct order
form elastic strain to a piezoelectric crystal causes its
of magnitude for strong piezoelectric crystals such as
electrical polarization. Therelectrical polarization is
segnet salt (4.2 1010 C/m2). In quartz, which is a weak
characterized by a vector P . Crystalline quartz is a
piezoelectric, eijk is about 1.5 109 C/m2.
well known example of a piezoelectric material. Math-
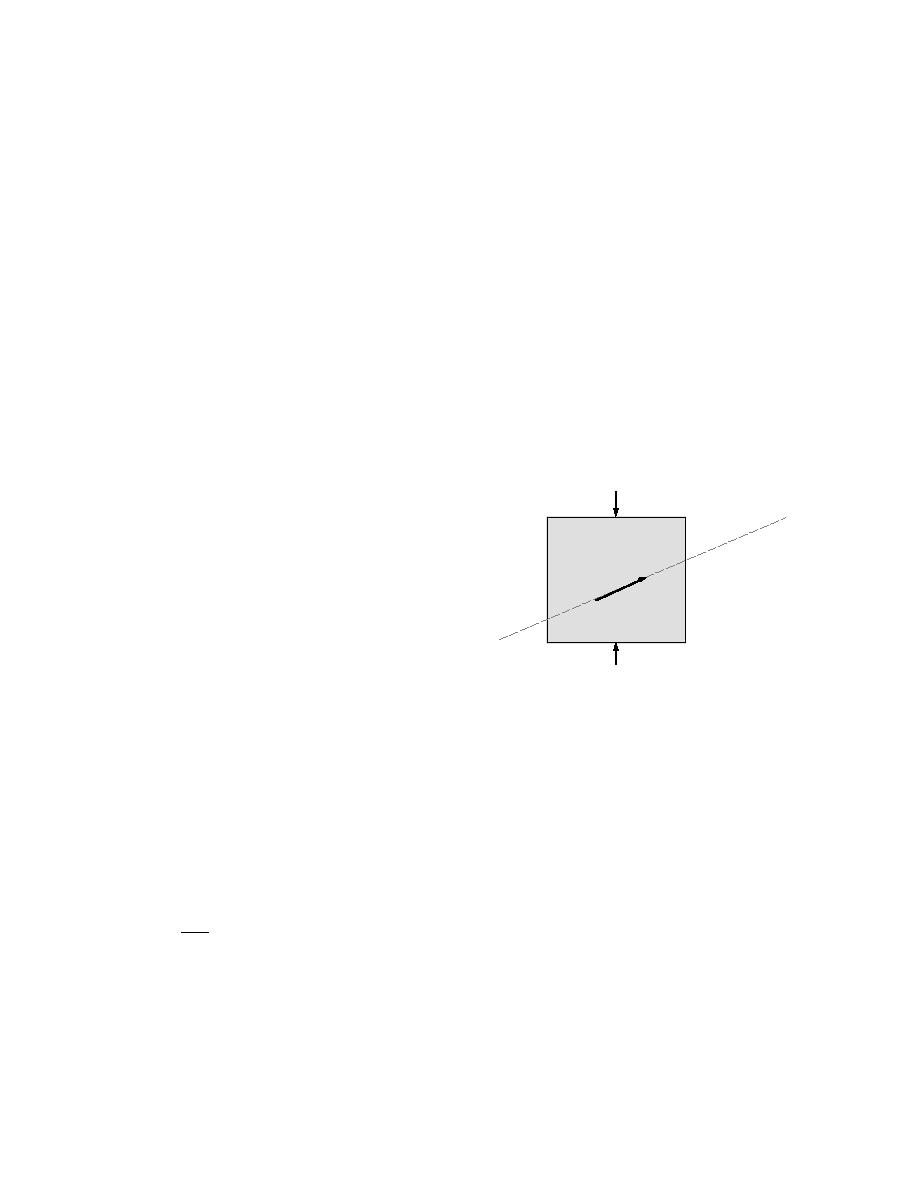
Figure 12r illustrates generation of the electrical
ematically, the direct piezoelectric effect is described
polarization P under the action of uniform compres-
sion. Looking at the figure, we can easily realize that
Pi = ε 0 χijEj + eijk ε jk
(14)
the piezoelectric effect is incompatir le with a center of
b
symmetry. Otherwise, the vector P would not know
ith component of the polarization vector
where Pi =
which direction to go: to the left or to the right. Accord-
eijk =
piezoelectric stress tensor
ing to Neumann's principle, the symmetry of any
χij =
electrical susceptibility tensor
physical property of a crystal cannot be less than the
εjk =
strain tensor.
symmetry in the atomic structure of that crystal. In our
case this means that crystals with a center of symmetry
The inverse effect produces a contribution to the strain
in the atomic structure cannot exhibit a piezoelectric
effect.
εmn = cmnijσij + dkmn Ek
(15)
σ
where cmnij = stiffness tensor
and
xis tion
σij = stress tensor
a
ial
c
pec ial dire
s
dkmn = piezoelectric strain tensor.
c
spe
Two piezoelectric tensors relate
P
Pi = eijk εjk+(ε0 χ ijEj)
dkmn = smnij ekij
(16)
where smnij is the compliance tensor.
The physical mechanism of piezoelectric polariza-
σ
tion is very simple and can be explained in the following
Figure 12. Generation of piezoelectric polariza-
way. The atomic structure of all piezoelectric crystals
tion in a crystal under the action of the uniform,
may be thought of as consisting of pairs of positive and
uniaxial compression.
negative ions. Since one such pair makes an electric
dipole, we can say that the whole structure of a piezo-
Let us apply Neumann's principle to ice. Ice is a
electric crystal is composed of such elementary
molecular crystal consisting of water molecules. While
dipoles. Now, using this simplified interpretation of
the centers of the water molecules are arranged into a
piezoelectric polarization, we can easily estimate its
regular wurtzite lattice, the molecular dipoles may have
absolute magnitude, which can later be compared with
one of six allowed orientations and are not ordered (see
the magnitude of pseudo-piezoelectric effects in ice.
Hobbs 1974 and Petrenko 1993c). Such a random ori-
Let us take a typical length of an elementary dipole a =
entation of the dipoles results in zero polarization of ice
1010 m and the dipole concentration N = 3 1028 m.
as it is shown in Figure 13b. In other words, ice has a
Then
kind of statistical center of symmetry. An application of
uniform strain, as shown in Figure 13c, may cause
Nae
P≈
≈ 2 1010 C/m2 .
(17)
some reorientation of a small fraction of the molecules
ε0ε
but without distortion of the center of the symmetry
Application of a strain εii varies the length a by the
(Petrenko and Ryzhkin 1984b). The reorientation of
factor of εii. The piezoelectric polarization is described
water molecules in ice under strain is responsible for
with the change in the polarization vector
the ice anelastic relaxation. We can conclude now with
∆P ≈ εiiP.
(18)
piezoelectric. Though some early papers reported ob-
servation of a piezoelectric effect in ice (see, for in-
Hence, the components eijk of the piezoelectric
stance, Rossman 1950), it is likely that this resulted
10




 Previous Page
Previous Page
