σ
In ice Ih:
P = Σ pi = 0
P = Σ pi = 0
water molecule
+
pi
_
+
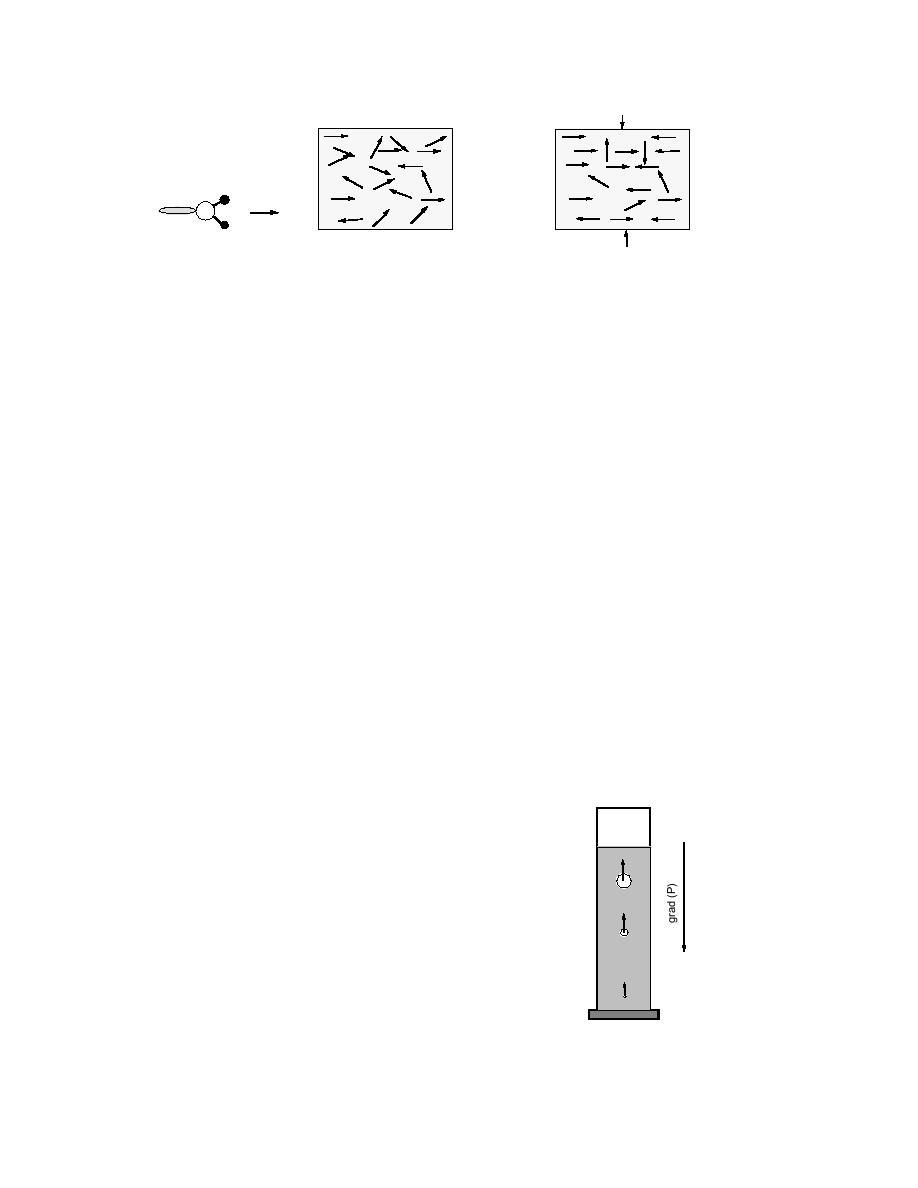
a. Electric dipole moment
b. Chaotic orientations of water
c. Partial ordering of the water mole-
of a water molecule.
molecules in ice before stress.
cules in ice after stress was applied.
Figure 13. Application of Neumann's principle to ice.
sure gradient in the same way as an air bubble moves
from some of the pseudo-piezoelectric effects dis-
upwards in water (Fig. 14). The reason for such migra-
cussed later in this report.
tion of the defects is that their specific volume differs
from that of a water molecule. As the result, point de-
Phonon-induced polarization of ice
fects larger then a water molecule will migrate in the
Whalley and Klug (1984) noticed that while a
direction opposite to the pressure gradient, while those
macroscopic bulk of ice does not have a dipole mo-
with a smaller specific volume will migrate in the direc-
ment, at the microscopic scale of about of tens of ang-
tion of the gradient. Some important practical cases in
stroms, the ice lattice may be polarized by statistical
which nonuniform strain causes the protonic defect's
fluctuations in the small statistical ensembles. That
migration and an associated electrical polarization are
means that at the microscopic scale ice can behave as a
shown in Figure 15. Also, since there is an oscillating
piezoelectric. As Whalley and Klug showed, this can
gradient of pressure in a longitudinal wave, such a wave
affect propagation of elastic waves with a wavelength
is followed by a wave of weak electrical polarization in
comparable to the size of the polarized micro-regions.
ice.
The same phenomenon should also result in additional
The formation of any protonic point defect results in
absorption of infrared light.
deformation of the surrounding lattice. In the case of
Bjerrum defects, the defective hydrogen bonds are
Polarization induced by nonuniform strain
weaker than the normal ones, and therefore they will be
Though ordinary ice Ih is not a conventional piezo-
longer. This is obvious in particular for a D-defect,
electric, under some special conditions elastic strain
where there exists an extremely strong repulsion be-
can induce an electrical polarization in it. Such special
tween two protons on one hydrogen bond. Accordingly,
conditions are gradients of strain, temperature or im-
we can assume that Bjerrum defects "expand" ice,
purity concentration and also an externally applied
increasing its volume. If ice is under pressure P, then the
electrical field. All these factors destroy the statistical
formation energy of the ith defect Eai is increased by the
center of the symmetry, whose existence imposes a
ban on the conventional piezoelectricity of ice.
Let us start the consideration of such pseudo-piezo-
electricity from an electrical polarization of ice caused
by nonuniform strain. This phenomenon was first ob-
served by Evtushenko et al. (1984), who have studied
electrical fields generated by bending vibrations in
thin pure single crystals of ice. Later (Evtushenko et al.
1987, Evtushenko and Petrenko 1991) such polariza-
tion was measured in a wide temperature range, from 0
to 80C, on ice doped with HF, HCl and NH3. The
wide temperature range and the doping were used to
study the phenomenon of ice having different types of
majority charge carriers. Also, a theoretical model of
the pseudo-piezoelectric effect was developed, which
Figure 14. Air bubble migra-
is explained below.
tion against a pressure gradi-
It was suggested that in ice under a nonuniform
ent in water.
strain, protonic charge carriers migrate along the pres-
11




 Previous Page
Previous Page
