ζ
of unstable stratification tends to homogenize the pro-
1 - φm (ζ′)
∫
ψ m (ζ) =
dζ′.
files; both wind speed and temperature bend more to-
(98)
ζ′
wards the vertical with increasing height. In stable con-
0
ditions, on the other hand, the stratification suppresses
We can follow exactly the same procedure with the
vertical exchange. Consequently, steeper gradients are
potential temperature and specific humidity gradients
possible.
in eq 78b and 78c to obtain the profiles of these vari-
From eq 9193, 97, 99 and 100, we see that the bulk
ables
transfer coefficients are clearly stability dependent (e.g.,
Andreas and Murphy 1986)
t
Θ(z) = Ts + * [ln(z / zT ) - ψ h (ζ)]
(99)
k2
k
=
CDr
(102)
[ln(r / z0 ) - ψ m (r / L)]2
[
]
q
Q(z) = Qs + * ln(z / zQ ) - ψ h (ζ)
(100)
k2
k
=
CHr
[ln(r / z0 ) - ψ m (r / L)] [ln(r / zT ) - ψ h (r / L)]
where
ζ
1 - φh (ζ′)
(103)
∫
ψ h (ζ) =
dζ′.
(101)
ζ′
k2
CEr =
0
.
[ln(r / z0 ) - ψ m (r / L)] [ln(r / zQ ) - ψ h (r / L)]
To see the ψm and ψh functions that result from inte-
grating the φm and φh functions that I described in the
(104)
last sections, see Paulson (1970), Lettau (1979),
At neutral stability (r/L = 0) both ψm and ψh are zero
Holtslag and de Bruin (1988), Arya (1988, p. 166 f.),
by definition. Such conditions define the neutral-
or Launiainen and Vihma (1990).
stability bulk transfer coefficients. From eq 102104,
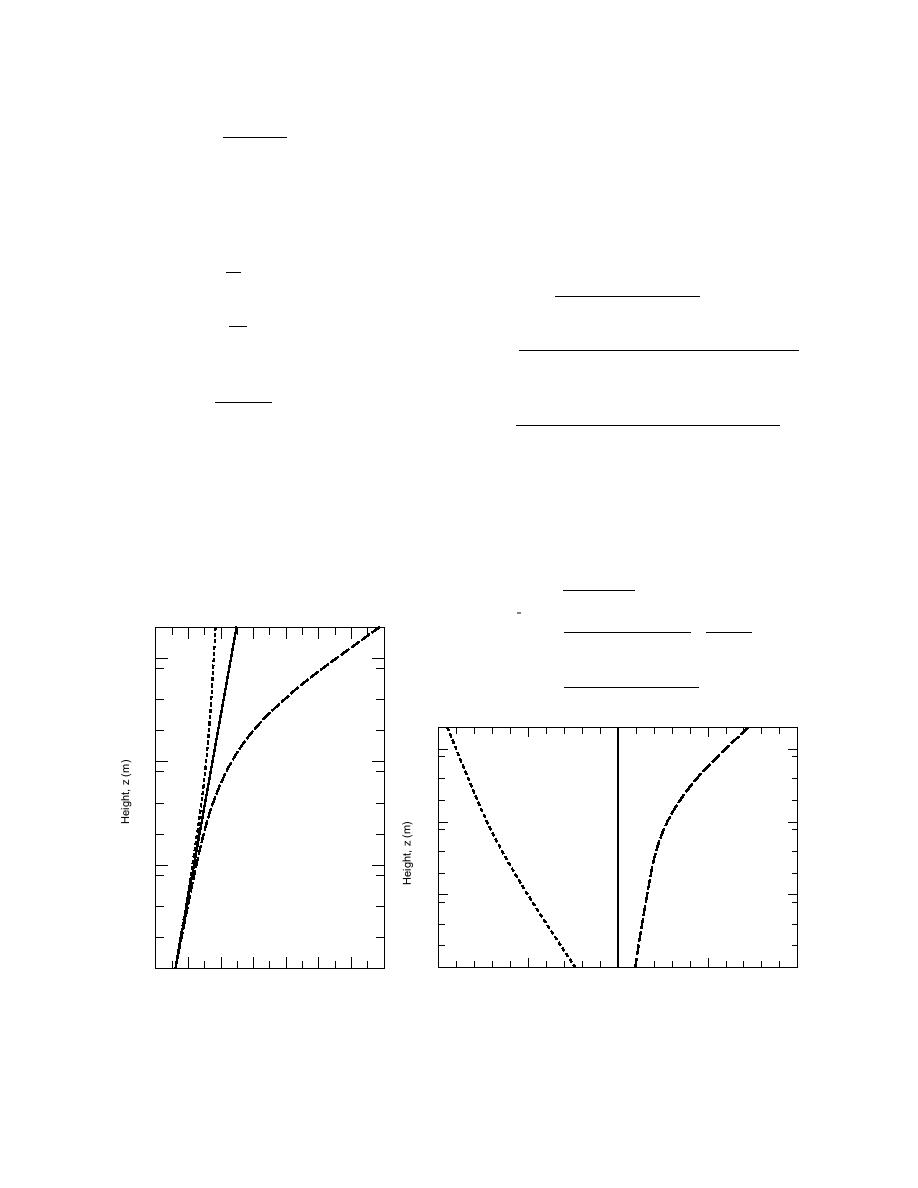
Figures 6 and 7 show sample wind speed and poten-
these are
tial temperature profiles computed from eq 97 and eq 99.
k2
Note the curvature of the unstable wind speed and tem-
=
CDNr
(105)
perature profiles. The vertical exchange characteristic
[ln(r / z0 )]2
k CD/Nr
12
k2
=
=
20
CHNr
[ln(r / z0 )][ln(r / zT )] ln(r/zT )
10
CDNr
( nstable
Neutral
(
Stable
(106)
=
L = 2 m)
L = 2 m)
1 k 1 CD/Nr ln(zT / z0 )
12
20
10
(
Stable
Unstable
(
eutral
1
tL = 2 m,
tL = 2 m,
= 0.1C)
= 0.5C)
*
*
,z
U
1
t, z
N
0.1
0.1
z
u = 0.20 m /s
*
= 1.0 10 3 m
0
0.01
0.01
20
15
10
5
0
0
2
4
6
8
10
12
14
Potential Temperature, θ (C)
Wind Speed, U (m /s)
Figure 7. Sample potential temperature profiles. Conditions are
Figure 6. Sample wind speed profiles. Condi-
as labeled. The ψm in eq 97 is based on the Businger-Dyer form
tions are as labeled. The ψm in eq 97 is based
(eq 79 and Figure 4) for the unstable case and on the Dutch formula-
on the Businger-Dyer form (eq 79 and Figure
tion (eq 83 and Figure 5) for the stable case.
4) for the unstable case and on the Dutch for-
mulation (eq 83 and Figure 5) for the stable case.
15




 Previous Page
Previous Page
