Consequently
SURFACE-LAYER PROFILES
Neutral stratification
u
U(z) = * ln(z / z0 )
(72)
Long before the advent of Monin-Obukhov similar-
k
ity theory, turbulence researchers used scaling arguments
to model the wind speed profile in neutral stratification.
the familiar semi-logarithmic form of the wind speed
As I explained, u* is the fundamental velocity scale in
profile in neutral stratification.
the ASL, and z is a fundamental length scale. In neutral
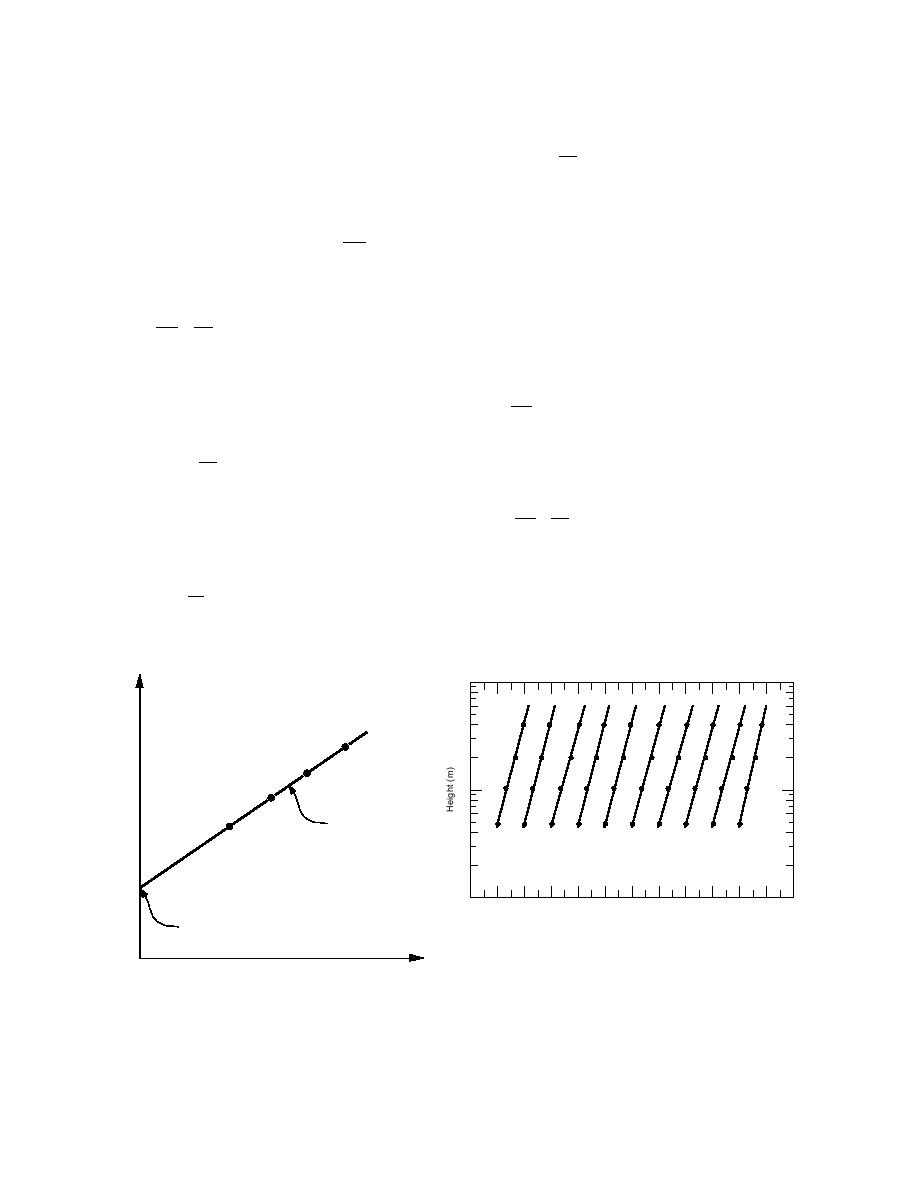
Figure 2 is a schematic interpretation of eq 72. If we
stratification (i.e., when L is infinite or wtv is zero), these
measure U at several heights and plot these data in a
coordinate system that is logarithmic in z, the data
are the only scales available to us. Consequently, the
vertical gradient in wind speed must obey
should lie on a straight line. The slope of this line is
u* / k ; it intersects the U = 0 axis at ln z0.
dU u*
=
Equation 72, however, is not just a theoretical con-
(69)
dz k z
struct. Semi-logarithmic wind speed profiles are fairly
common in nature. Figure 3 shows 10 of the 197 such
where k, the von Krmn constant, assures the equality.
profiles that Andreas and Claffey (1995) observed over
The no-slip boundary condition means that U(z) is
sea ice in the western Weddell Sea.
zero at the surface. Hence, we can integrate eq 69 easily
If wtv is small enough that conditions are still near
to obtain
neutral though t* (i.e., the sensible heat flux) is non-
zero, the potential temperature profile obeys the same
u
U(z) = * ln z + b
(70)
scaling as in eq 69. Because t* is the appropriate tem-
z
perature scale
where b is an integration constant. Because of the
dΘ t*
=
.
logarithm on the right side of eq 70, we cannot write
(73)
dz k z
U(z = 0) = 0. Rather, we define a new length scale, the
roughness length z0, where U(z = z0) = 0. Thus
There is no reason to assume a priori that the same
multiplicative coefficient k1 should appear in both eq
u
b = - * ln z0 .
69 and 73. In fact, the Kansas results (Businger et al.
(71)
k
1971) showed not only that k = 0.35--rather than the
more common value of 0.40--but also that there should
be an additional multiplicative constant of value 0.74
Ice Station Weddell
Semi- Logarithmic Profile
10
1
u
Inz
*
Slope =
k
8651 8647 8684 8631 8636 8689 9614 8685 8686 7633
.
.
.
.
.
.
.
.
.
.
24
24
0
5
1
5
2
5
3
5
4
5
5
5
6
5
7
5
2
3
0.1
0
2
4
6
8
10
12
14
16
18
20
22
24
Wind Speed (m/s)
Inz 0
Figure 3. Hourly averaged, semi-logarithmic wind speed pro-
files observed on Ice Station Weddell (Andreas and Claffey
U
0
1995). The lowest level of the left-most profile is assigned a value
Figure 2. Schematic representation of the semi-
of 2 m/s; subsequent lowest levels are offset by 2 m/s. Thus, these
profiles reflect relative rather than absolute values. The lines
logarithmic wind speed profile.
are least-squares fits according to eq 72. Under each profile, the
upper number is the extrapolated value of the wind speed (in
m/s) at 10 m; the middle number is the Julian day in 1992; the
lower number is GMT.
10




 Previous Page
Previous Page
