dQ q*
φh (ζ).
=
on the right side of eq 73. Wieringa (1980), however,
(78c)
dz k z
reexamined the Kansas data, concluded that k = 0.41,
As in our earlier discussion, these φ functions--
nearly the traditional value of 0.40, and found no need
for an additional multiplicative constant in eq 73.
though presumably universal--are empirical: They
must be found experimentally. Notice, I use the same φ
Hgstrm's (1988) review suggested k = 0.40 0.01
and, again, that eq 69 and 73 represent correct scaling
function in both the temperature and humidity equa-
in neutral stratification. Henceforth, I eschew the pop-
tions because there is no good theoretical reason why
ular Kansas results and take the more traditional but
these should be different (Hill 1989). A definitive ex-
observationally defensible position that k = 0.40 and
periment that verifies this assumption, however, has not
that the von Krmn constant is the only factor neces-
been done, though several experiments support it (e.g.,
sary in both eq 69 and 73.
Dyer 1974, Dyer and Bradley 1982).
For unstable conditions, φm and φh are fairly well
As we did with eq 69, we can integrate eq 73 from
the surface to height z. The result is
known (e.g., Paulson 1970)
t
φm (ζ) = (1 - 16ζ)
-1 / 4
Θ(z) = Ts + * ln z + c
(74)
(79a)
k
-1 / 2
φh (ζ) = (1 - 16ζ)
where Ts is the surface temperature, and c is a constant
.
(79b)
of integration. As in eq 71, we find c by requiring Θ to
be Ts at the surface; thus
These are commonly called the Businger-Dyer relations
because Joost Businger (1966) and Arch Dyer derived
t
Θ(z) = Ts + * ln(z / zT )
(75)
them independently in the mid-1960s (Businger 1988).
k
Though the constant multiplying ζ in eq 79 may vary
where zT is a new length scale, the roughness length
somewhat among the various experimental evaluations
of φm and φh (e.g., Dyer and Hicks 1970, Businger et
for temperature.
Exactly the same arguments that we used to predict
al. 1971, Wieringa 1980, Dyer and Bradley 1982,
the potential temperature gradient also apply to spe-
Hgstrm 1988), the same basic functional form comes
cific humidity. Thus, in near-neutral stratification
through.
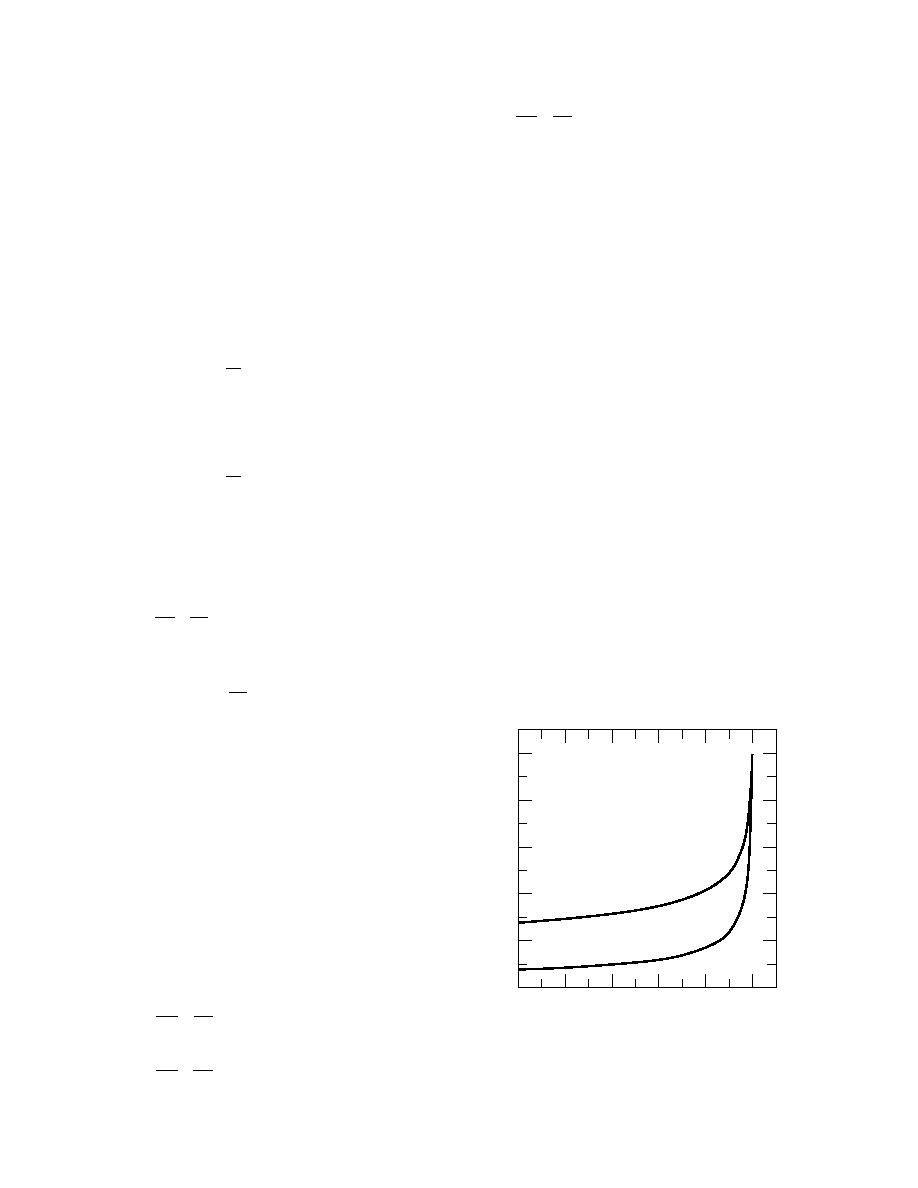
Figure 4 shows eq 79 as functions of stability.
dQ q*
=
Notice in the figure and in eq 79, φm = φh = 1 at ζ = 0
.
(76)
dz k z
(i.e., for neutral stratification) as eq 69, 73, and 76 re-
quire. Figure 4 also shows that as ζ gets larger--as
Integrating this yields
conditions become more unstable--both φm and φh
q
Q(z) = Qs + * ln(z / zQ )
(77)
k
where Qs is the surface value of the specific humidity,
and zQ is yet another length scale, the roughness length
1.0
Unstable
for humidity. z0, zT and zQ are not necessarily equal, as
I will explain later.
0.8
Including stratification effects
Because atmospheric stratification is rarely near
0.6
neutral, it often affects the shape of surface-layer pro-
files. Thus, eq 69, 73 and 76 are not strictly accurate in
diabatic conditions. We can extend these, however, on
φm = (1 16 ζ) 1/4
0.4
the basis of Monin-Obukhov similarity theory. These
diabatic profile corrections, in fact, are at the core of
0.2
Monin and Obukhov's (1954) work. They simply tried
φh = (1 16 ζ) 1/2
to retain the basic form of eq 69, 73 and 76 by multi-
plying these by functions that depend only on z/L
0
10
8
6
4
2
0
dU u*
φm (ζ)
=
ζ = z/L
(78a)
dz k z
Figure 4. Nondimensional wind speed and scalar gra-
dients, φm and φh, as functions of stability for unstable
dΘ t*
φh (ζ)
=
(78b)
conditions.
dz k z
11




 Previous Page
Previous Page
