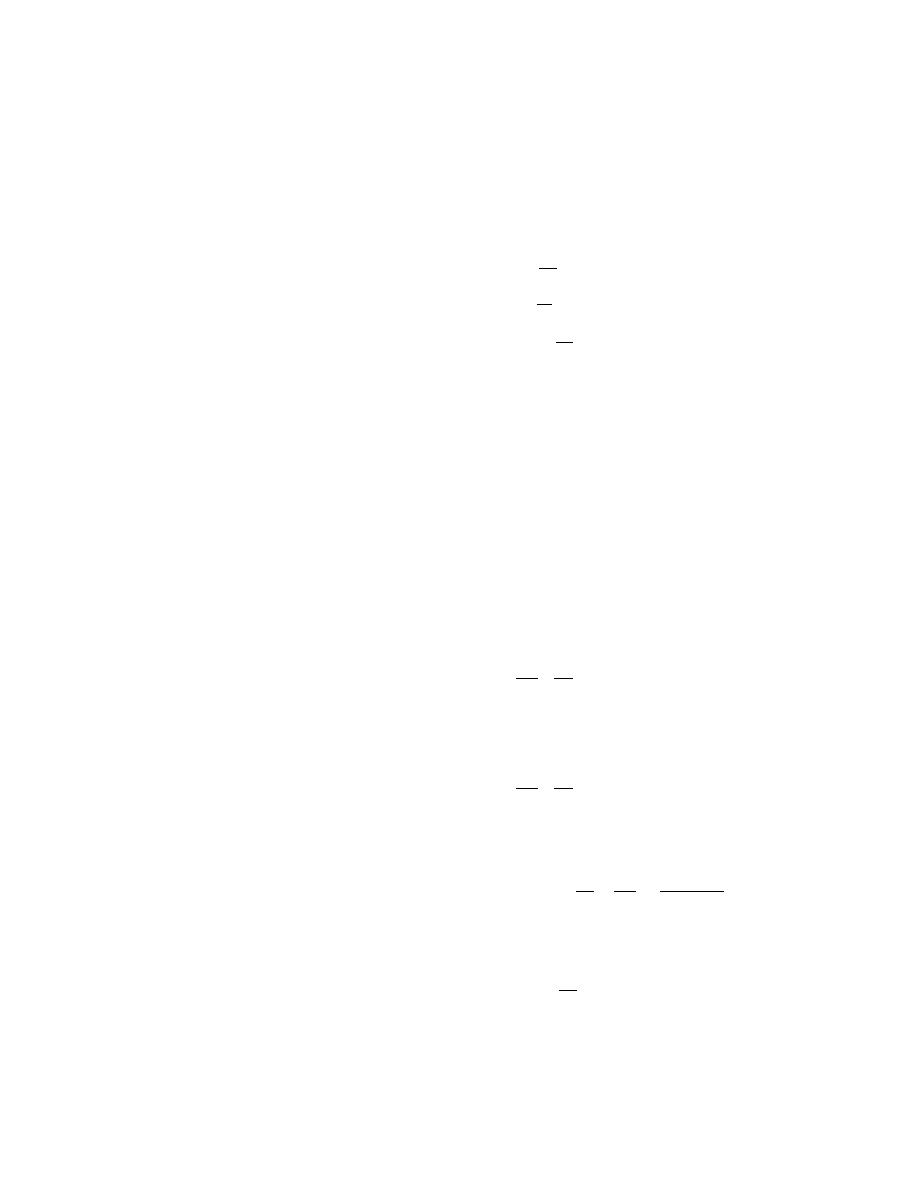
Table 1 also shows the Deacon numbers that the four
data, in computer models, and for some analytical stud-
φm and φh formulations in Figure 5 predict in very
ies, it is often convenient to know the so-called bulk
stable conditions.
transfer coefficients. These relate a turbulent flux to
Table 1 yields contradictory suggestions as to which
more readily available quantities.
of the φm and φh formulations is best in stable condi-
Here, I will discuss the bulk transfer coefficients for
tions. The Webb (1970) and Wieringa (1980) functions
momentum (usually called the drag coefficient) and
predict that Ricr is 0.20 and 0.14, respectively--roughly
for sensible and latent heat. These are defined, respec-
the traditional range for Ricr (Lumley and Panofsky 1964,
tively, as
p. 117). The Dutch formulation predicts Ricr = 1.4, a
τ = -ρ uw = ρu* = CDr ρUr2
2
value in line with more recent appraisals. The critical
(91)
Richardson number based on Lettau's (1979) formula-
Hs = ρcp wt = -ρcpu t = CHr ρcpUr (Ts - Θ r )
tion is unbounded, a result that Monin and Yaglom
(92)
**
(1971, p. 441) defended theoretically and that Lettau
HL = ρLv wq = -ρLvu q = CEr ρLvUr (Qs - Qr ). (93)
believed was possible in light of his South Pole obser-
**
vations.
In very stable conditions, turbulence is suppressed;
In these cp =
specific heat of air at constant pressure
the vertical exchange of heat and momentum must thus
Lv =
latent heat of vaporization or sublimation
be by molecular processes alone. In such conditions, the
Ts, Qs =
surface values
Ur, Θr, Qr =
vertical profiles of wind speed and temperature depend
values at some reference height, usually
linearly on height, and their vertical gradients are, thus,
10 m
constants with height; Dm and Dh would then be zero.
CDr, CHr = bulk transfer coefficients. Since these are
Viswanadham's (1982) analysis also suggested that zero
and CEr height dependent, I explicitly include a
is the limiting value, at least for Dm, in very stable con-
height subscript in their symbols.
ditions. (He did not consider Dh.) In Table 1, three of
the formulations predict that zero is the limit for the
In the last section, I introduced the gradient func-
tions φm(ζ) and φh(ζ) in eq 78. These let us quantify Ur,
Deacon numbers in strong stability. But, again from his
Ts Θr and Qs Qr in eq 9193 and thereby provide a
measurements at South Pole, Lettau (1979) found that
Dm = 1/4 and Dh = 1/2 in very stable conditions and,
mathematical framework for handling the bulk trans-
therefore, tuned his φm and φh functions to produce these
fer coefficients. Take wind speed as an example. From
limits.
eq 78a
In stable stratification, wave phenomena can supplant
dU u*
forced convection and molecular diffusion as the domi-
=
φm (z / L).
(94)
nant mechanisms for transferring heat and momentum.
dz k z
These processes are necessarily intermittent. The strati-
Panofsky (1963) and Paulson (1970) showed how to
fication builds and builds, until a wave breaks and in-
integrate this. The trick is to write
troduces new turbulence that episodically homogenizes
the wind speed and temperature profiles. The overrid-
dU u*
[1 - 1 + φm (ζ)]
ing stratification eventually damps this turbulence until
=
(95)
the cycle repeats. Thus, it seems that all the limiting
dz k z
Deacon and Richardson numbers listed in Table 1 may
be appropriate at times. The very steep temperature gra-
then the integration becomes
dient that Lettau (1979) reported would be consistent
z
with a relatively quiet, strongly stratified surface layer.
ζ
U(z)
1 - φm (ζ′) ′
u* dz′
∫
∫
∫
dζ .
dU ′ =
-
But the weaker gradient of the Dutch formulation seems
(96)
k z
ζ′
plausible, too, in a surface layer frequently mixed by
z0
U(z0 )
0
breaking gravity waves. Thus, the stable atmospheric
surface layer is still rife with interesting questions about
Hence, because U(z0) = 0
turbulence processes.
u
U(z) = * [ln(z / z0 ) - ψ m (ζ)].
(97)
k
BULK TRANSFER COEFFICIENTS FOR HEAT
AND MOMENTUM OVER SEA ICE
Thus, the trick in eq 95 leads again to a semi-
logarithmic profile with an additive stability correction.
Mathematical background
That stability correction in eq 97, ψm, is defined as
For estimating turbulent surface fluxes from field
14




 Previous Page
Previous Page
