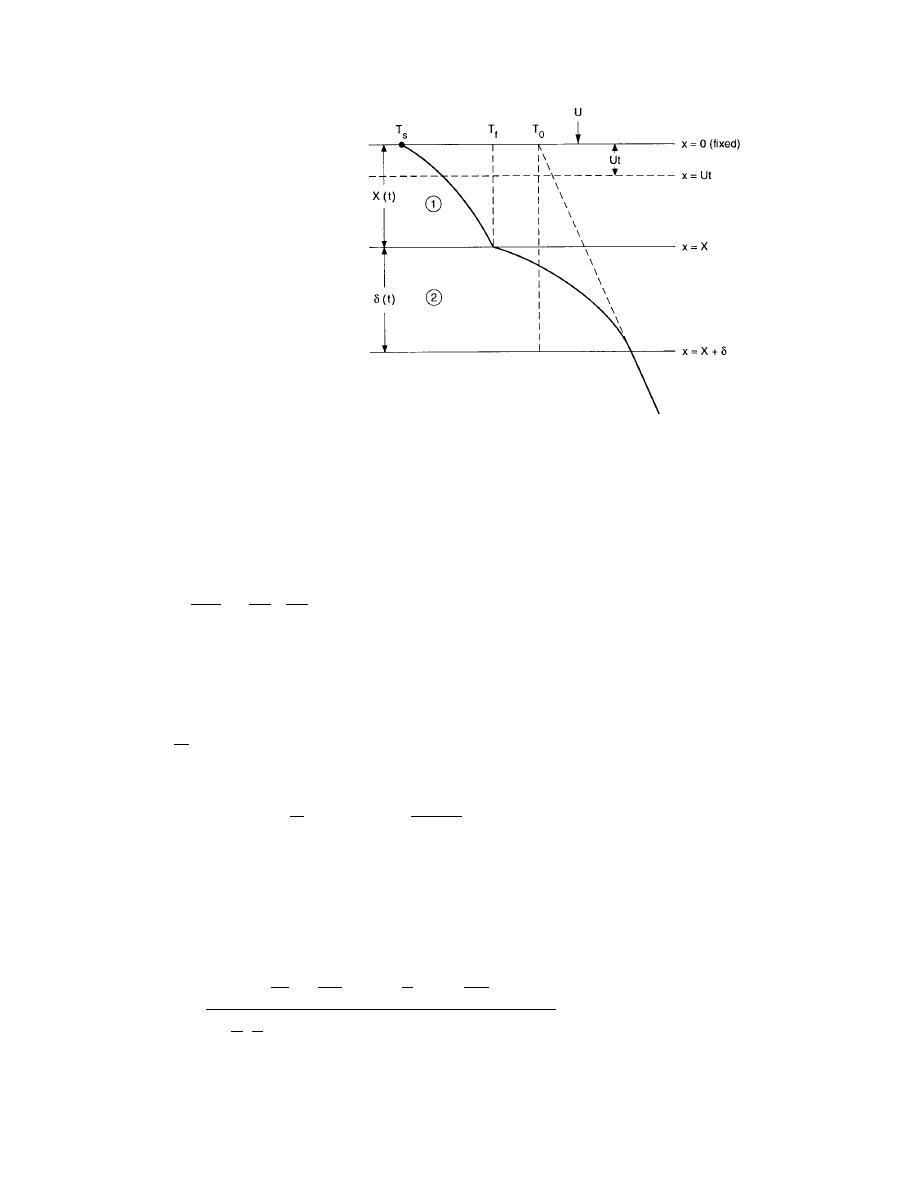
Figure 14. Coordinate system for stationary upper surface.
Thus, at some time during the formation process, the bottom must be melting to compensate for the deposi-
tional growth but the process cannot be steady.
Let us fix the upper surface so that it remains stationary, as shown in Figure 14. Then it would appear
that a steady flow of material is moving at a constant velocity U and the original soil surface seems to be
moving downward at a steady velocity. The energy equation is transformed such that a convective term ex-
ists. The equations for regions 1 and 2 are
2
Ti
T
T
αi
-U i - i = 0
i = 1, 2.
(25)
x2
x
t
The boundary and initial conditions are exactly the same as those of the heterogenetic case (see Appendix
C for details of the syngenetic equations).
The heat balance integral form of the energy equations is
X+δ
X
{ρ1c1 T1( x, t)dx + ρ2c2
∫ T2 ( x, t)dx - ρ1lX + (ρ2c2 - ρ1c1)Tf X
d
∫
dt
X
0
(26)
T (0, t)
-ρ2c2 ( X + δ)To + ( X + δ) = -k1 1
[
]
G
+ k2G - ρ1c1U∆T1 - ρ2c2U ∆T + G( X + δ) .
x
2
We note that this is identical to the relation for heterogenetic growth, eq 5, except for the two additional
terms on the right-hand side of eq 26. Carrying out the integrations and making eq 26 nondimensional,
leads to the following result.
σ
τ = ∫ K1dσ
(27)
0
1
σg′
2
C21 σ + φ σβ′
(
)
b1 + b2β -
- C21σ β + 1 -
1 -
6g
g
3
3
K1 =
(28)
1 1
{
]}
[
- 2 + k21 - ψ 1 + 1 / ST + C21 φ + σ(β + 1)
σg
where
13



 Previous Page
Previous Page
