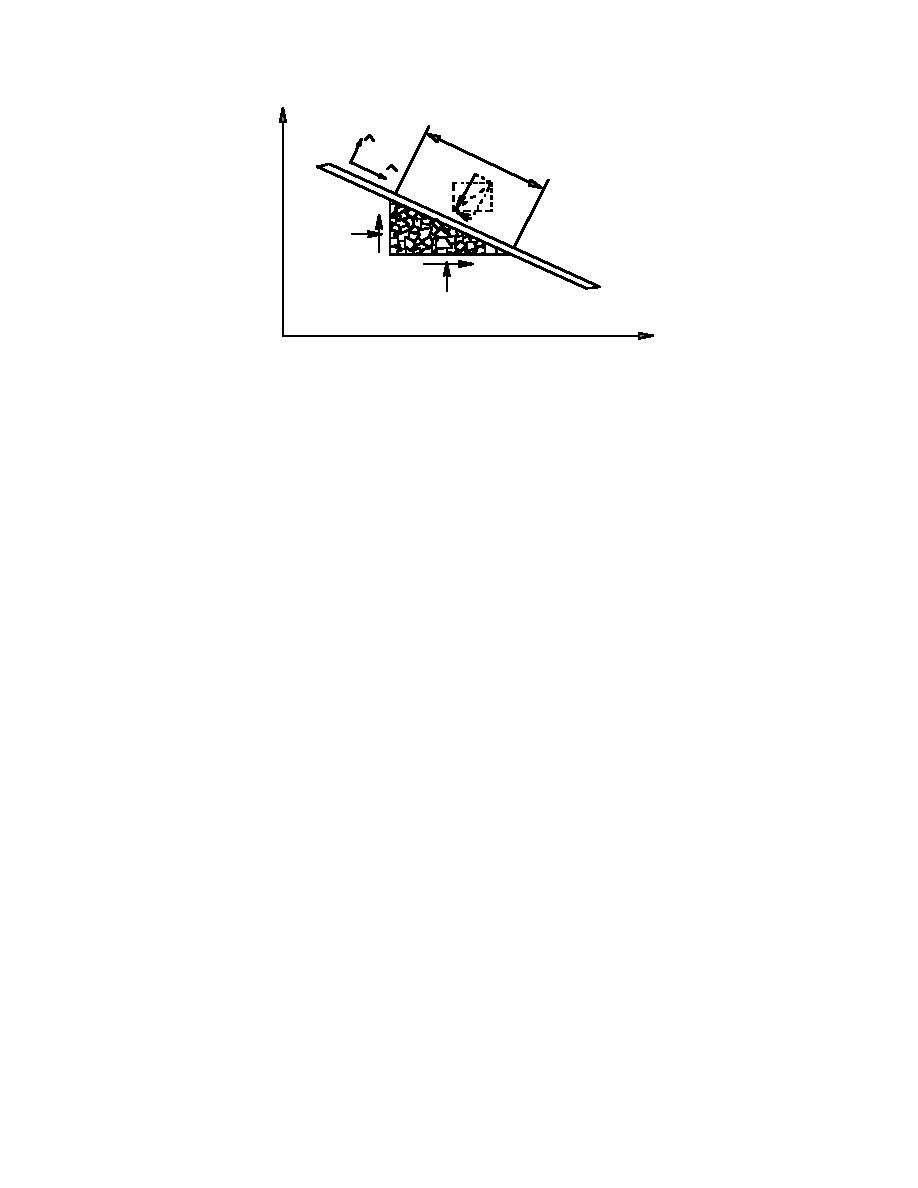
y
dl
n
σn
t
Y
σ xy c
X
σt
σxx
boo m
a
b
σ yx
σ yy
x
Figure 5. Interaction of a differential element of ice rubble with the boom.
MODEL VERIFICATION AND CALIBRATION
in which
Verification of the hydrodynamic model with
X and Y = x- and y-components of the ice load on the
a uniform ice cover
boom
N = ice concentration
The hydrodynamics model is verified by simulating
τsx,τsy = components of wind drag in x- and
flow in a rectangular ice-covered channel of length 2000
y-directions
m, width 500 m, bed elevation at upstream 5 m, bottom
τwx,τwy = components of water drag in x- and
slope 0.0001, and bed Manning's coefficient of 0.03.
y-directions.
The ice cover thickness is selected to be 1.06 m, with a
Manning's coefficient 0.03. Water discharge is 2500
Since the ice element is essentially stationary, the force
m3/s and downstream water surface elevation is 0.2
balance conditions ∑ Fx = 0 and ∑ Fy = 0 reduce the
m. The simulated water surface profile is compared with
above equations to the following, by neglecting the
the result of the one-dimensional backwater calculation
higher order terms
in Figure 6.
X = σ xx cos( n, x ) + σ yx cos( n, y )
(43)
Analytical solutions for river ice jams
Y = σ yy cos( n, y ) + σ xy cos( n, x ) .
(44)
Analytical solutions for idealized ice jams in a
straight, uniform, rectangular channel with a uniform
The normal and shear stresses acting on the boom
current are developed for verifying the numerical model.
segment ab are
The numerical simulation results are compared with
analytical solutions for ice accumulation in a channel
σ n = σ xx cos2 (n, x) + σ yy cos2 (n, y) +
of length 5000 m, width 500 m, constant water velocity
(45)
of 0.6 m/s, and zero water surface slope. A boom is
+ 2σ xy cos(n, x) cos(n, y)
placed at 500 m and assumed 100% effective, i.e., no
ice is allowed to pass it. Initially, 900 ice parcels of size
σ t = (σ yy - σ xx ) cos(n, x) cos(n, y) +
(46)
50 50 m having a thickness of 0.2 m and a
+ σ xy cos2 (n, x) - σ yx cos2 (n, y) .
concentration of 0.6 are placed over the water surface
from the upstream boundary and the boom. In the
The normal and tangential components of the load per
simulations, this ice cover was allowed to move and
unit length of the boom are
consolidate behind the boom under the action of the
Pn = Ntiσ n
current drag. No additional ice was added during the
(47)
simulations. The model parameters used are
Pt = Ntiσ t .
summarized in Table 1.
(48)
10




 Previous Page
Previous Page
