For soils, p is often taken as the mean effective stress
p', taking into account the pore water pressure, u:
p' = p - u .
(9)
2. Deviatoric stress, also called the Mises equiva-
lent stress, or the octahedral shear stress, which de-
termines distortion:
(I
)
2
q = τoct =
+ 3I2 =
2
2
J2
(10)
1
9
3
.
3. An additional deviatoric stress measure, t (HKS
1998):
LM
IJ FG J3 IJ 3 OP
FG
1
1
q
H
K H q K PQ
t = 1+ - 1-
MN
(11)
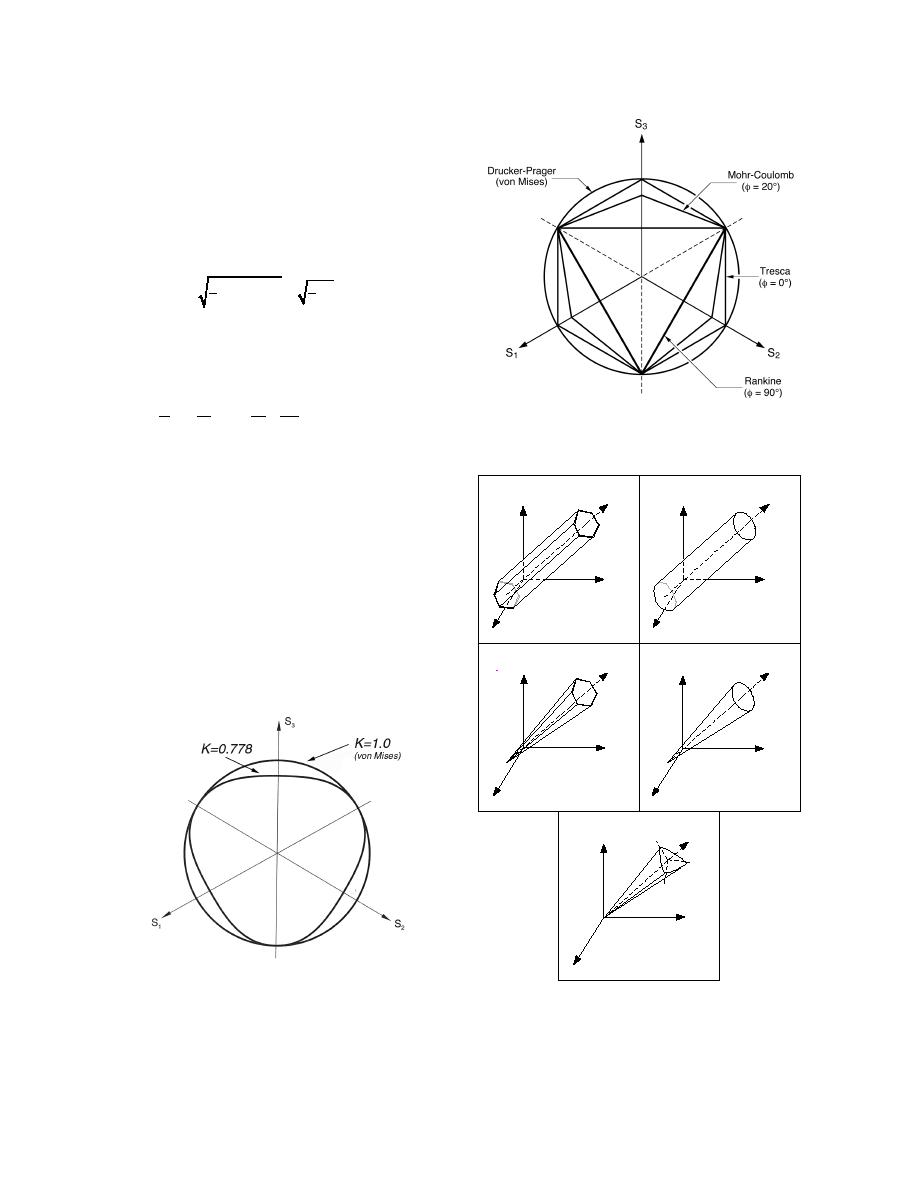
Figure 10. Yield surfaces in deviatoric space.
2
K
K
(After HKS 1998.)
where K is a material parameter (between 0.778 and
Hydrostatic
Hydrostatic
1.0) that controls the yield dependence on the third
σ1
σ1
Axis
Axis
stress invariant and defines the shape of the yield
surface in the deviatoric plane. The K value allows
for different stress failures in tension and compres-
sion. For K = 1, the yield surface is circular (von
σ3
σ3
Mises yield), as shown in Figure 9, and the failure
stress is the same in tension and compression. K is
limited to values of 0.778 or greater for the surface to
σ2
σ2
Tresca
von Mises
remain convex. Some of the more common failure
surfaces are shown in Figure 10 in deviatoric space
Hydrostatic
Hydrostatic
σ1
Axis
Axis
σ1
and in Figure 11 in principal stress space.
σ3
σ3
σ2
σ2
Mohr-Coulomb
Drucker-Prager
Hydrostatic
σ1
Axis
σ3
σ2
Lade
Figure 9. Modified DruckerPrager yield sur-
Figure 11. Common yield surfaces along the hy-
face in deviatoric space. (After HKS 1998.)
drostatic axis in principal stress space. Caps
defining compactive failure are not shown. (After
Shen and Kushwaha 1998.)
7



 Previous Page
Previous Page
