law (Fig. 14). In cases where exponential hardening
Cap plasticity models incorporate both the com-
is not a good fit, as is common in soils, the hardening
pression and shearing of the material. Critical state
law can also be represented in a piecewise linear ap-
models are a type of cap model where a critical state
proach using the experimental data (Fig. 15).
line (csl) is located at the peak of the yield surface
and divides material yield by compaction on one side
and yield by dilation on the opposite side. The mate-
rial deforms at a constant volume at the critical state.
The critical state line (curve) in three-dimensional
space defined by normal compressive stress p', devia-
toric (shear) stress q, and specific volume v is shown
in Figure 12. For simplicity in gathering the model
parameters, the yield surface is generally viewed in
planar form in the compressive plane (vp or vln p)
or the deviatoric plane (p'q or pt).
Hardening law
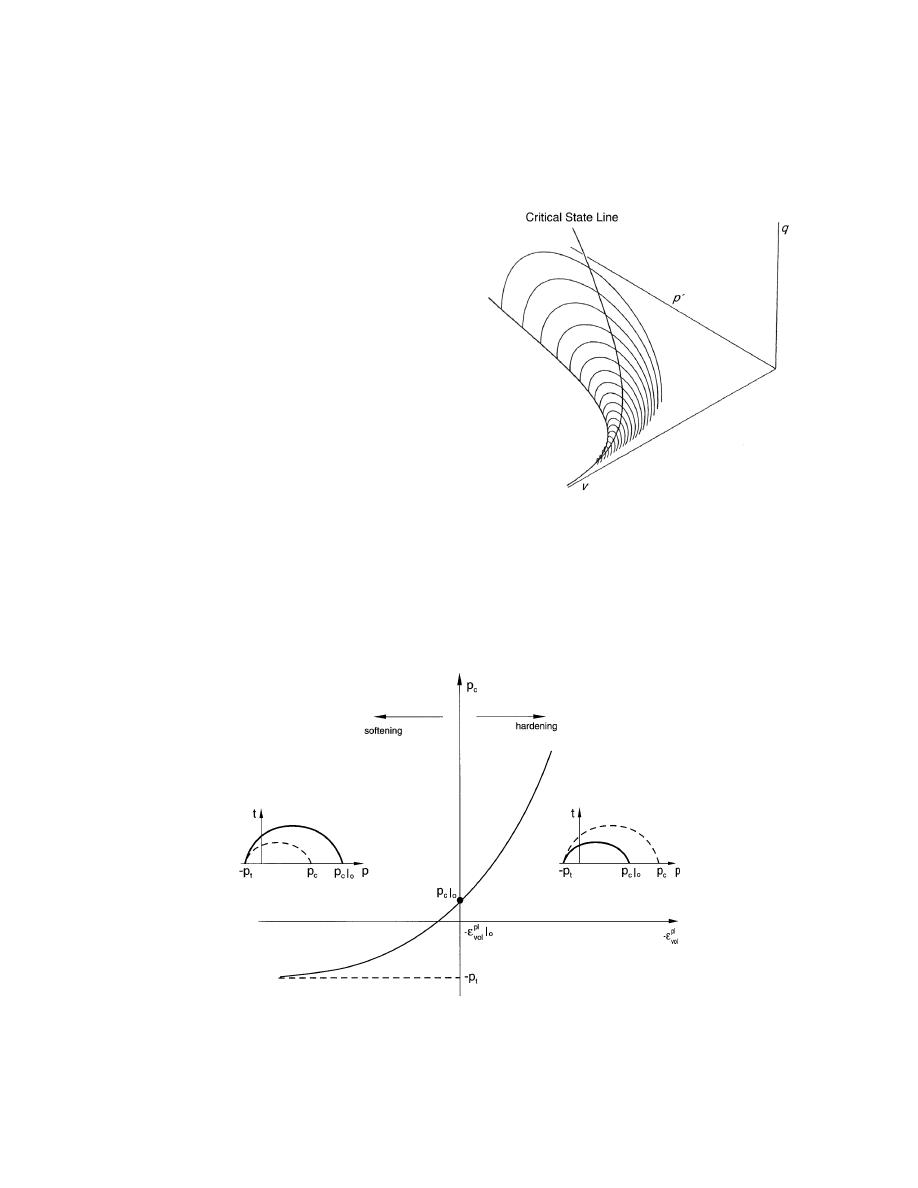
The cap on the yield surface defines the compac-
tivedilatant behavior of the material failure as the
cap expands and contracts (Fig. 13). The cap is gen-
erally spherical or ellipsoidal, and the material either
hardens or softens by expanding or contracting the
cap. This behavior is defined in the pressure-volume
relationship called a hardening law. The pressure
Figure 12. Three-dimensional view of critical state
volume relationship is often exponential and there-
yield surface. The critical state line defines failure
at constant volume. (After Wood 1990.)
fore can be modeled using an exponential hardening
Figure 13. Cap contraction or expansion reflecting the softening (left)
or hardening (right) of the material. (After HKS 1998.)
8



 Previous Page
Previous Page
