pressure acts equilaterally within the ice and the impu-
R (cos θ)1
rities concentrations are similar, then heat is directed
towards the veins and the lenses will disappear. Impu-
rities in the veins are potentially mobile, however, and
Ice
thus mL may exceed mv in the contaminated region of
Water
the sample. Heat is then directed toward the colder
θ
lenses and the veins will shrink. If mL = 2mv and rv =
100 m, the equilibrium lens radius is 13 m. Thus
while lenses may form, it is unlikely that they will grow
large enough to coalesce. We must also consider the
R
possibility that the stress does not act equilaterally. Nye
and Mae (1972) observed the formation of lenses and
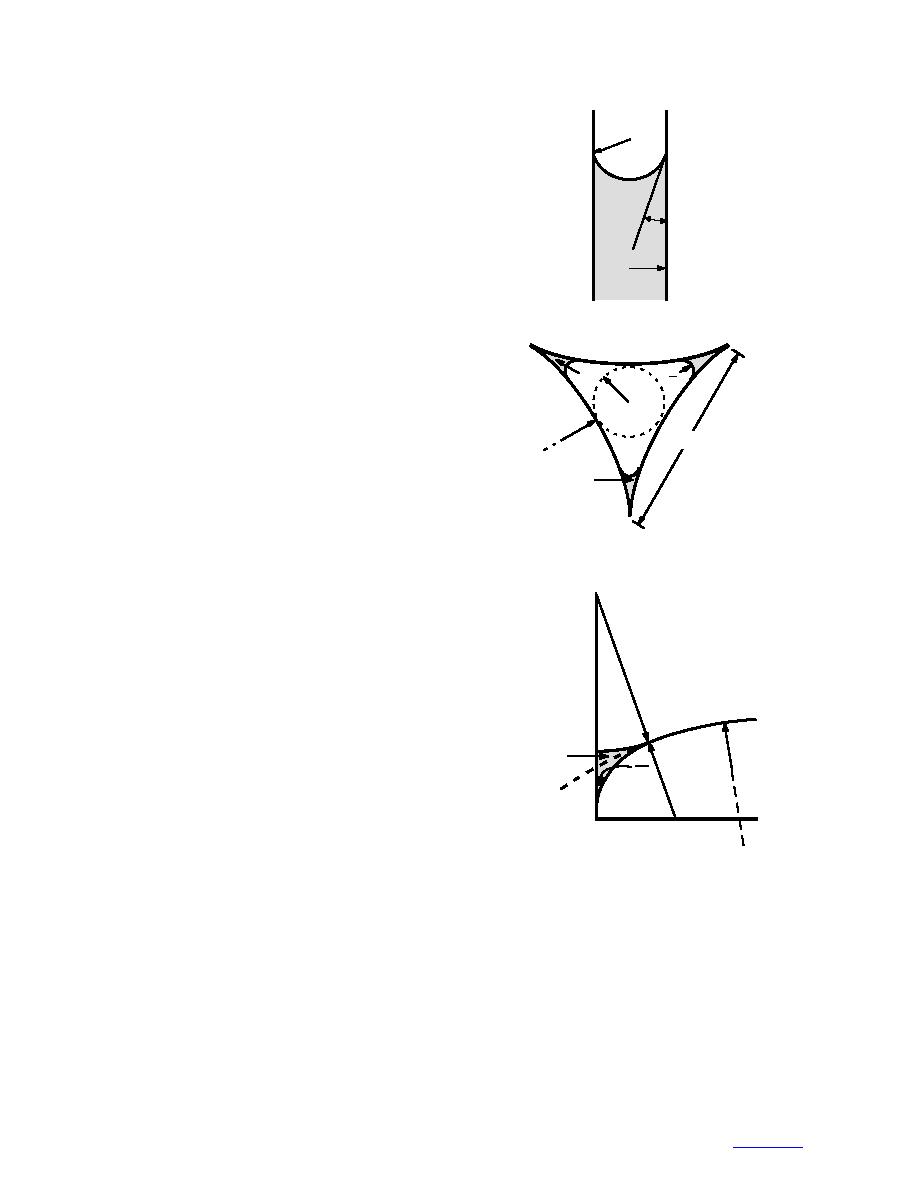
a. Air/liquid interface within a cylinder.
shrinkage of veins following the short application of a
compressive stress of 1.3 bar. They theoretically com-
Ice
pute a critical overburden pressure of 0.23 bars for this
rAv
φ
A
2
rAv
effect to occur.
In this paper we investigate unsaturated ice and, thus,
must also take into the account the thermodynamic state
dv
of ice when the vapor phase is present. In many ways,
rv
the saturated and unsaturated regimes in ice are analo-
gous to the funicular and pendular regimes in snow
Water
(Colbeck 1973, Morris 1993). Here we conceptualize
ice as a porous medium, similar to snow or soil, where
the pores are either vein segments or nodes. Each pore
b. Air-entry radius of curvature with-
has a critical entry pressure that must be reached before
in a vein and hypothesized location
air can replace water. For a cylindrical pore of radius
of liquid in an unsaturated vein.
R, the radius of curvature of the air/liquid interface is
R/cosθ, where θ is the contact angle (Fig. 8a). Without
defining in detail the geometry of the interfacial sur-
face in a vein, we specify an equivalent hemisphere
β
whose radius rAv is that of an inscribed circle (Fig. 8b).
ra
Although veins have a flared, trumpet-like shape at the
surface (Nye 1991b), here we consider only interior
veins with parallel faces. If the contact angle is 0, the
pressure drop across the interface is pa pl = 2σal /rAv,
where σil is the surface tension (0.075 J m2) and rAv =
Ice
rv
Water
φ
0.2273 dv (Table 1). This pressure drop defines the air-
rg
2
entry pressure PAv as
PAv = 0.6600/dv
(5a)
where PAv is in Pascals and dv in meters. A column of
c. Grain-boundary groove.
air replaces water in the vein when the pressure drop
exceeds PAv. We note that air columns of smaller radius
Figure 8. Geometry of liquid inclusions in contact
with air (not to scale).
not touching the ice faces are mechanically unstable.
The newly formed cylindrical meniscus is of higher
PWv = 0.3300/ dv.
(5b)
tension than the hemisphere and immediately retreats
into the three grain-boundary vertices, as shown in Fig-
The configuration shown in Figure 8b is not in mechani-
ure 8b. Water inclusions in the unsaturated regime thus
cal equilibrium. We discuss potential changes in ice
consist of concave triangular columns in the grain-
curvature in the following paragraph. Similarly, we use
boundary grooves. Water cannot refill the vein until the
the radius of the inscribed sphere within a node to com-
gauge pressure is lowered to the point PAv/2 where the
pute its air-entry pressure PAn. Using the nodal geom-
menisci again touch. Thus the water re-entry pressure
etry determined by Nye (1989),
is half the air-entry value:
7



 Previous Page
Previous Page
