2000
1600
H = 0.07
0.06
1200
Q(H,L)
(m3 /hr)
0.05
800
0.04
400
0
2
4
6
8
10
L, Weir Length (m)
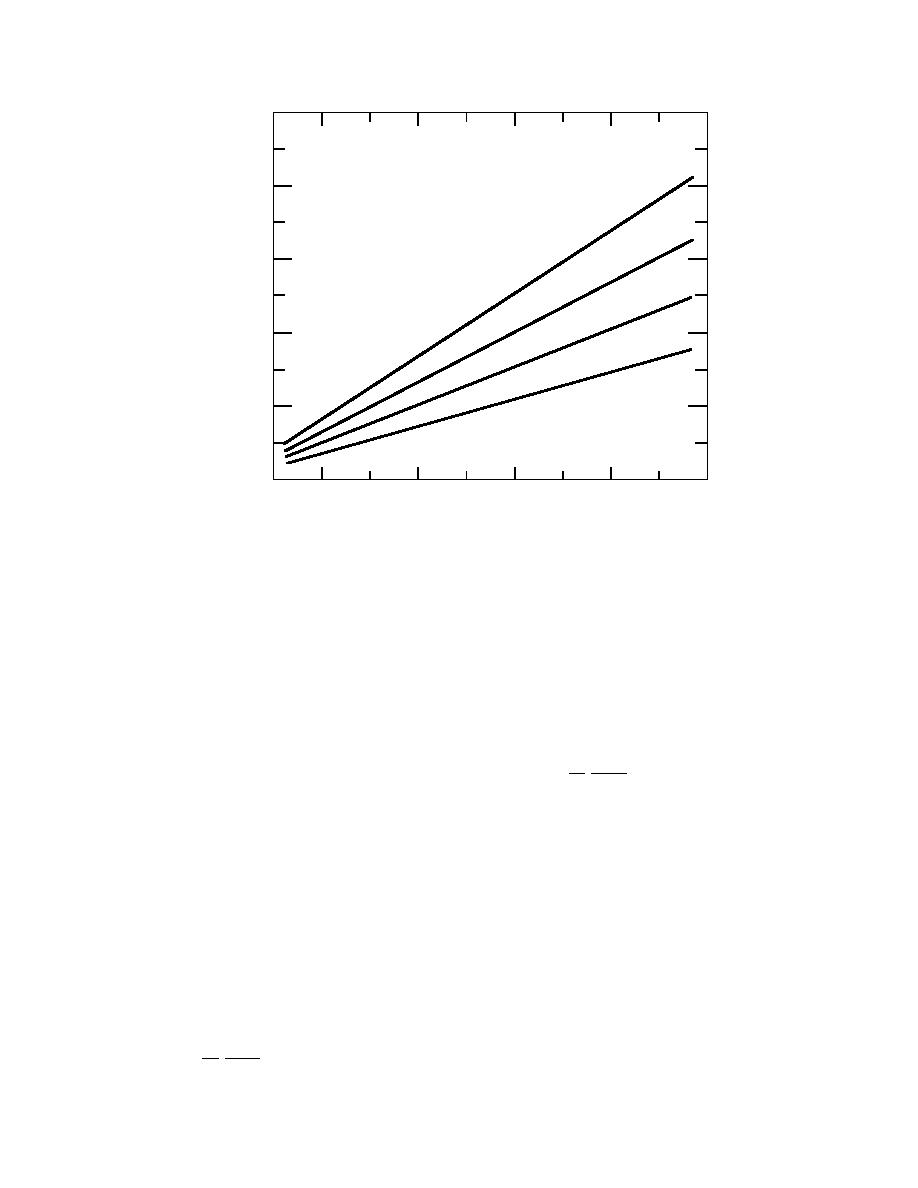
Figure 6. Instantaneous weir flow rates for various heads.
the previous calculations:
Now we can look at drainage times (in hours)
as a function of weir length:
H = 0.04, 0.05 ... 0.07 (m)
P = 0.15 (m), g = 9.81 (m/s2)
L = 2.44, 3.94, ... 9.5 (m)
L = 1.2, 1.3 ... 9.7 (m)
Q(H) = (9144) [L 0.2(H)] (H)1.5 (m3/hour) (3a)
Q(H) = (9144) [L 0.2(H)] (H)1.5 (m3/hour). (3a)
V(H) = (8094) H (m3)
(4a)
The instantaneous effect of head on flow rates over
the weir is illustrated in Figure 6. This, of course,
1 V(H )
t = ∫0..005
0 076
is a linear relationship. We can now look at the
dH (hours).
(5a)
H Q(H )
time-required-to-drain relationship for a given
weir length. The following relationships are used:
Evaluating this integral yields the graph in
L = 3.05 (m)
Figure 7.
To confirm this analysis, we can look at Hicks'
Q(H) = 9144 [L 0.2(H)] (H)1.5 (m3/hour) (3a)
analysis of the variation in head on a weir with-
out inflow to the reservoir, essentially what we
V(H) = (8094) H (m3).
(4a)
have here. The formula used in Hicks (1972) is
t = [2A/CL] (1/h20.5 1/h10.5) (hours)
An integral was developed to derive the time
(6)
required to drain based on the flow (Q): volume
(V) relationship. It is integrated over the change
where
in head over the fixed weir:
A = pond area (m2)
C = 1.83, the discharge coefficient
H1 1 V(H ) dH
t=∫
H2 H Q(H )
(hour).
(5)
L = weir length (m)
10



 Previous Page
Previous Page
