500
800
1:1
400
1:1
600
300
400
200
200
100
0
0
0
200
400
600
800
1000
1200
100
200
300
400
500
0
Height of Inversion, zi (m)
z Ri (m)
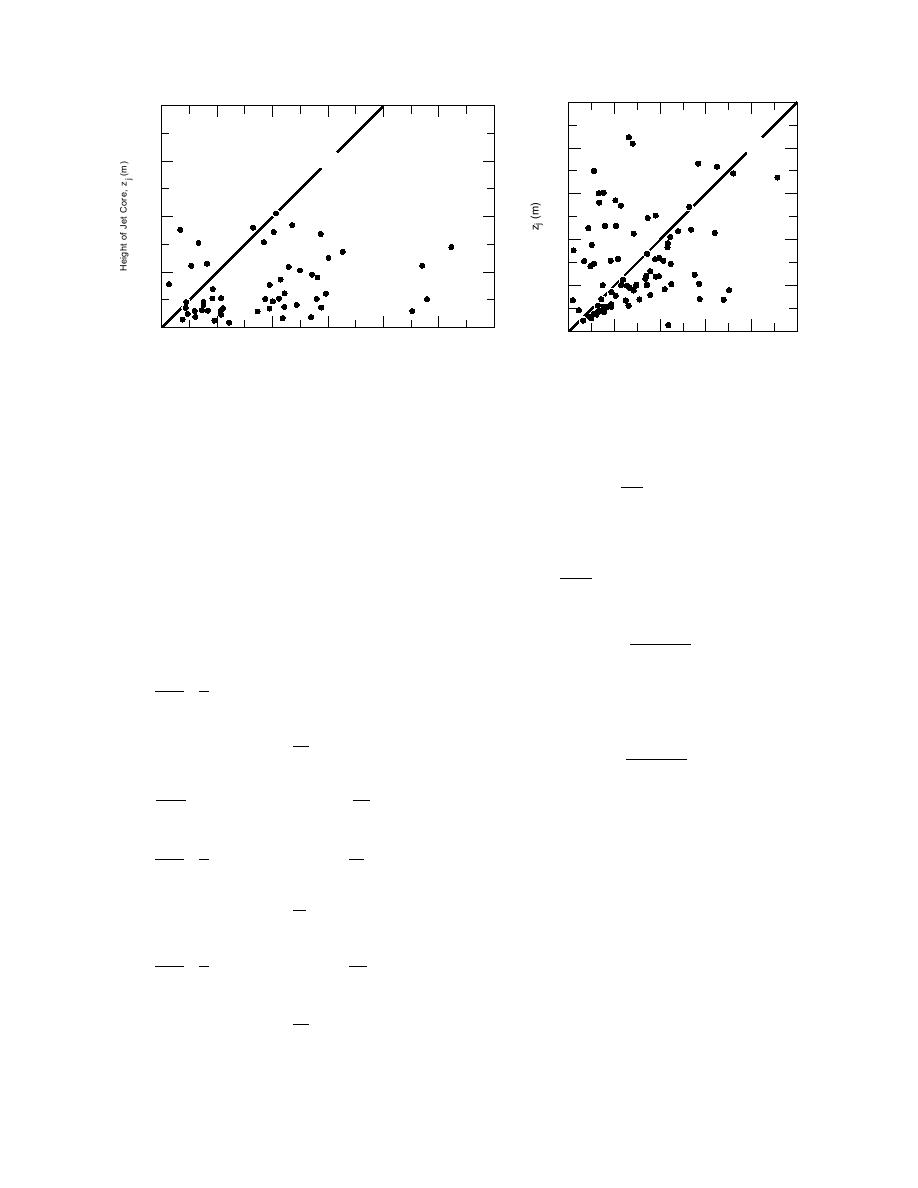
Figure 26. Observations of the height of the
Figure 25. Observations of the height of the core of the low-level
jet core (zj), a surrogate for h, versus the esti-
jet (zj) and of the corresponding height of the inversion (zi) on Ice
mated height of the turbulent layer from a
Station Weddell (Claffey et al. 1994, Andreas et al. 1995).
Richardson number criterion (zRi) (see eq 145
and 146) (Andreas et al. 1995).
^
A() ≡ ln(h / z0 ) -
kU
Now back to Rossby number similarity.
u*
Since eq 139141 and eq 142144 are two sets of
(150a)
expressions for the same quantities, there should exist a
= k FU (z / h, ) + ψ m () - ln(z / h)
height interval in which both sets are true. That is, as
z / z0 → ∞ (and z / zT → ∞, z / zQ → ∞ ) and as
-k V
^
sgnf = k FV (z / h, )
z / h → 0 , the two formal descriptions of the atmospheric
B() ≡
(150b)
u*
profiles should be simultaneously accurate (Blackadar
and Tennekes 1968, Tennekes 1982, Hess 1992). In these
(
)
^
k Ts - Θ
asymptotic limits, eq 139141 and eq 142144 require
C() ≡ ln(h / zT ) +
that
t*
(151)
[
]
= ln(z / z0 ) - ψ m (z / L)
U(z) 1
= k FΘ (z / h, ) + ψ h () - ln(z / h)
u*
k
(147a)
^
(
)
U
= FU (z / h, h / L) +
k Qs - Q
^
D() ≡ ln(h / zQ ) +
u*
q*
(152)
^
V (z)
V
= 0 = sgnf FV (z / h, h / L) +
= k FQ (z / h, ) + ψh() - ln(z / h).
(147b)
u*
u*
In each of these, the middle term does not depend
Θ(z) 1
[
]
= ln(z / zT ) - ψ h (z / L) + s
T
on z; consequently, although there is a z in the right
t*
t*
k
(148)
term, this term must be independent of z also. Like-
^
Θ
wise, because the right term depends explicitly on the
= FΘ (z / h, h / L) +
new stability parameter = h/L (first introduced by
t*
Kazanski and Monin 1960), the middle term must also.
Therefore, Rossby number similarity lets us define the
[(
]
)
Q
Q(z) 1
= ln z / zQ - ψ h (z / L) + s
new profile functions A, B, C and D that depend only
q*
t*
k
on . These functions are often called resistance laws
because they show how the bulk boundary layer
(149)
^
Q
= FQ (z / h, h / L) +
parameters U, V, θ, Ts , Q, Qs and h are related to the sur-
^ ^ ^
^
.
q*
face properties u*, t*, q*, z0, zT, zQ and L. In a way, A,
It is straightforward to rearrange and rewrite eq 147
B, C and D are thus comparable to the bulk transfer
149 as
coefficients CDr, CHr and CEr.
29




 Previous Page
Previous Page
