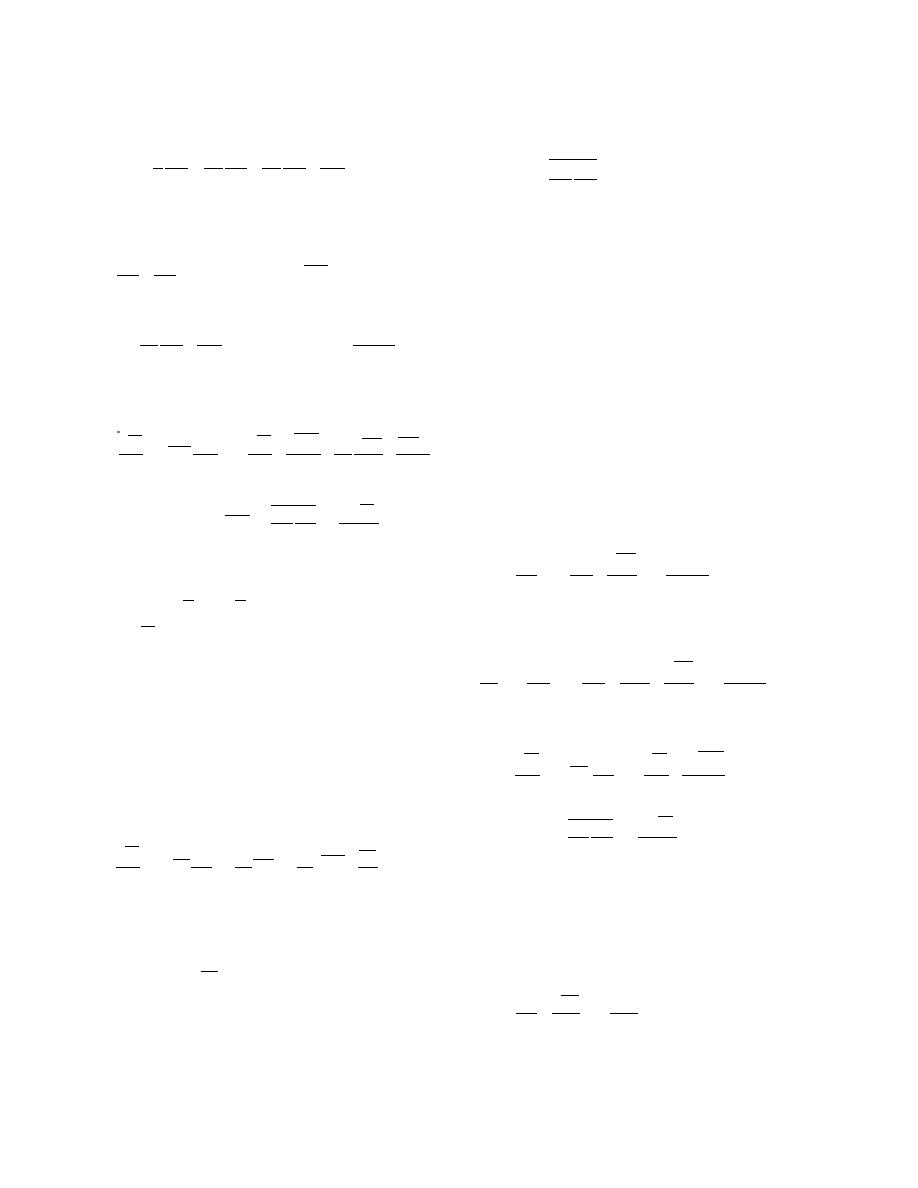
Consequently, term III in eq 4 is
ity fluctuations and the pressure fluctuations. Term V,
which is
~
1 p tv g
1 p
1 P
δ i3.
=
+
-
(29)
ui ui
ε≡ν
ρ xi ρ0 xi ρ0 xi
~
(34)
Tv
xj xj
With eq 29 substituted into eq 4, we subtract eq 12 to
is called the dissipation rate of TKE. Because in eq 34
ui/ xj is a squared quantity, ε is always positive. But
get an equation for the turbulent velocity component ui
since ε appears with a minus sign in eq 33, term V is
(
)
ui
+
Uiuj + uiU j + uiuj - uiuj
always a sink for TKE. It represents the dissipation of
t
xi
the turbulence to heat because of viscous effects.
In summary, eq 33 shows the processes that are im-
2
portant in maintaining the turbulence in an atmospheric
1 p tv g
ui
δ i3 - 2Ωε ijk ηjuk + ν
=-
+
.
surface layer. For example, for steady-state conditions,
(30)
ρ0 xi
Tv
xj xj
the turbulent transport terms in eq 33 (IV) are often small.
Multiply this equation by ui, then average. After some
Consequently, mechanical (II) and buoyant (III) produc-
manipulations, we get
tion nearly balance viscous dissipation (V). Production
equals dissipation (Panofsky and Dutton 1984, p. 92 ff.;
Fairall and Larsen 1986).
e2uj
e2
e2
1 ui p wtv g
Ui
= - uiuj
- Uj
-
-
+
Starting with the scalar conservation equations, eq 7
ρ0 x j
t
xj
xj
xj
Tv
and 8, we can follow a procedure similar to that above to
derive equations for scalar means and variances. With
potential temperature as an example, insert eq 9a and b
2 e2
ui ui
- 2Ωεijk ηj uiuk - ν
+ν
(31)
.
into eq 7 and average. The result is
xj xj
xj xj
ujθ
Θ
Θ
Θ
2
Here
+ Uj
+
=D
.
(35)
(
)
t
xj
xj
xj xj
1
1
e2 ≡
uiui = u2 + v2 + w2
(32)
2
2
Now subtract eq 35 from eq 7 to get a conservation
e2
and
is the average Turbulent Kinetic Energy (TKE).
equation for the turbulent temperature fluctuations
In eq 31, we henceforth ignore the last term on the
ujθ
ujθ
θ
Θ
θ
θ
2
right-hand side, the viscous transport term, because it is
+ uj
+ Uj
+
-
=D
. (36)
small except very near the surface. The Coriolis term in
t
xj
xj
xj
xj
xj xj
eq 31 is identically zero because εijkuiuk = uiuk ukui
Multiply this equation by θ and average
for all j.
Again invoking horizontal homogeneity in an atmo-
ujθ2
2
θ2
Θ
θ2
spheric surface layer (where W = 0) and assuming that
= -2ujθ
- Uj
-
the mean wind is in the x direction (i.e., V = 0), we fi-
t
xj
xj
xj
nally derive the turbulent kinetic energy equation from
eq 31
θθ
θ
22
- 2D
+D
(37)
.
xj xj
xj xj
2 wp
e2
U
g
- ε. (33)
= -uw
we +
wtv
+
ρ0
z
As in eq 31, we can ignore the molecular transport term,
t
Tv
z
the last term in eq 37. Again assume horizontal homo-
I
II
III
IVa
IVb V
geneity, that we are within a few tens of meters of the sur-
face (so W = 0), and that x is in the direction of the mean
Here, term I is the time rate of change of TKE. Term II
wind vector (i.e., V = 0). With these simplifications, the
represents mechanical production of TKE; the Reynolds
mean equation for potential temperature becomes
stresses (e.g., uw ) extract energy from the mean wind
speed gradient. Term III is the buoyancy production of
Θ
wθ
Θ
2
+
=D 2
(38)
TKE. Term IV shows that TKE changes because of tur-
t
z
z
bulent transport. Term IVa represents the vertical turbu-
lent advection of TKE; term IVb represents a transport
and the conservation equation for temperature variance
resulting from a correlation between the vertical veloc-
is
5



 Previous Page
Previous Page
