a jam. The static-unsteady thickness
2.4
solution presented earlier allows jam
Fully Coupled
thickness to fluctuate in time and space,
2.2
but the streamwise movement of the ice,
and therefore ice momentum, are not
Static-unsteady
2.0
included.
Early formulations of equilibrium jam
1.8
Equilibrium
thickness are based on uniform flow
depths and jam thickness in a reach of
1.6
0
1000
2000
3000
4000
5000
constant water surface slope. As a result,
x Location (m)
the force balance only contains the fol-
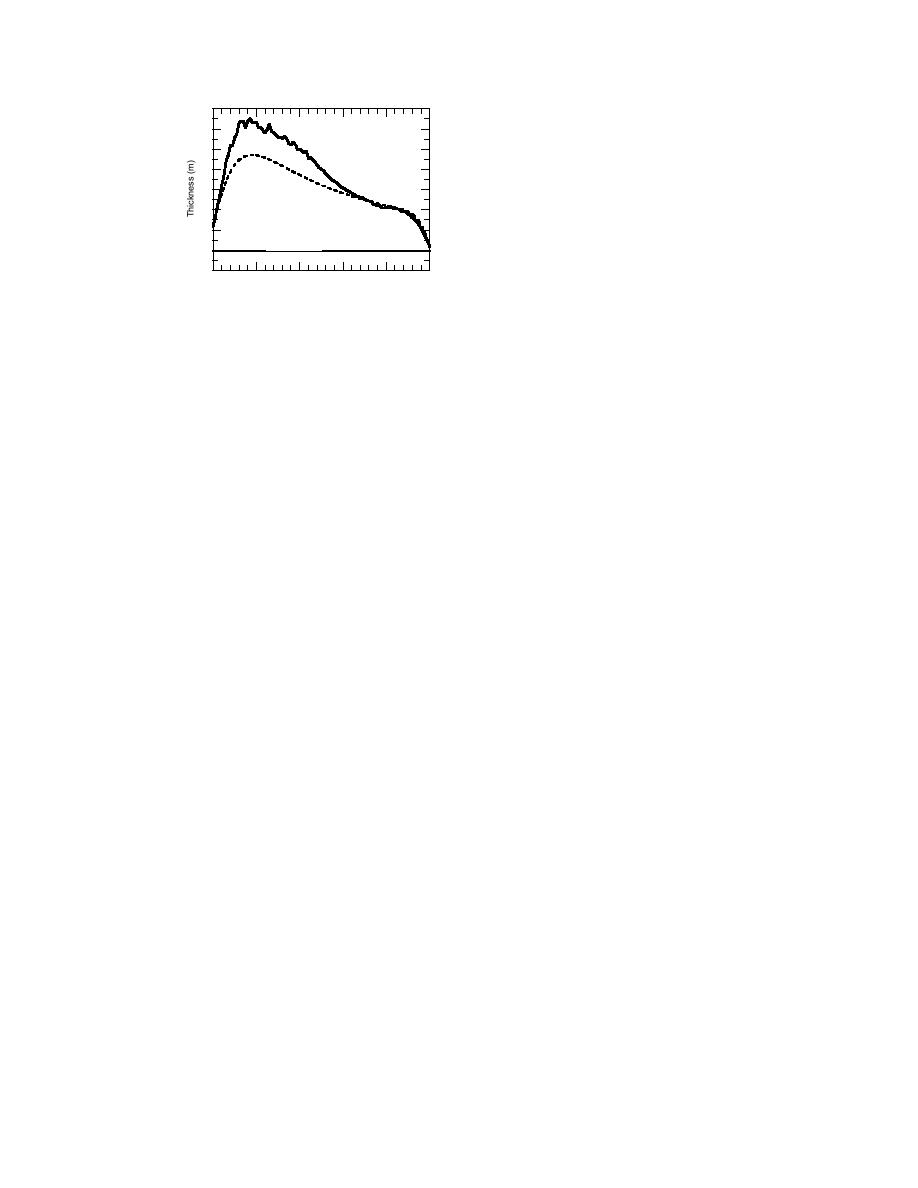
Figure 52. Comparison of thickness pro-
lowing terms: shear stress on the under-
file predicted by static-unsteady thickness
side of the jam from the water flow, the
model to fully coupled model and equilib-
downstream component of the gravity
rium thickness.
force on the jam (based on the bed slope
because of the uniform flow assump-
tion), and the shear resistance at the banks. Because the thickness is considered
uniform within the equilibrium reach, those formulations contain no terms reflect-
ing changes in hydrostatic pressure, jam strength, water depth, or jam thickness
along the reach considered. The formulation leading to eq 150, however, includes
these terms, but with the ice velocity terms reduced to zero. The resulting force
balance is affected by the nonuniform thickness of the jam as well as the nonuni-
form depths within a reach. The more complete balance of forces expressed in eq
150 enables more accurate modeling of jam profile, whether the profile includes an
equilibrium-thickness section or not.
To show the effects of ice momentum on jam thickness profile, the results of the
static-unsteady thickness solution leading to eq 150 were compared to those
obtained by the fully coupled model. The loosely coupled moving-ice model was
also run for the baseline conditions and compared to the fully coupled results to
demonstrate the effects of the coupling of the dependent variables on the jam thick-
ness profile.
The static-unsteady thickness model was run with the baseline inflow hydrograph
and all other parameters the same as for the baseline condition. Figure 52 shows
the predicted jam thickness profile obtained by the static-unsteady thickness model.
Also plotted are the thickness profile predicted using the fully coupled model and
force balance represented by eq 150 includes the partial derivative terms represent-
ing changes in jam strength and water surface slope along a reach. The changing
water surface slope becomes particularly important as discharge increases, increas-
ing the downstream-acting forces with a subsequent increase in jam thickness. With
a milder rate of increase in discharge, the water surface slope would remain closer
to the bed slope, resulting in a static-unsteady thickness profile nearer to the equi-
librium thickness. The importance of ice momentum is clearly evident from the
fully coupled thickness profile and results in much greater ice thickness. Ice veloc-
ity, and, hence, ice momentum, are greatest in the upstream reaches where the
increasing discharge wave is steepest. The ultimate arrest of this ice momentum is
responsible for the significantly greater thickness.
The effects of fully coupling the solution are determined by comparison with
the results from the loosely coupled model. The loosely coupled moving-ice model
was run with the inflow hydrograph and all other parameters the same as for the
68



 Previous Page
Previous Page
