TEST DATA

23 should be combined with eq 2a through 4.

TEST DATA

Then eq 1 can be written as

The validity of the temperature dependencies

τ *(p, ε, T) = τio (p, T)Φ(ε)

˙

i

of the strength parameters of ice presented above

was verified using test data of Gagnon and

Gammon (1995). The triaxial (σ2 = σ3) compres-

sion tests were carried out using cylindrical speci-

mens of Labrador iceberg ice, 9.58 cm in diameter

In the range of the hydrostatic pressures p <<

and 26 cm long. Mean grain diameter d ≈ 8.1 mm.

σmax, eq 24 takes the form

The test temperature varied between 1C and

16C. The tests were conducted at constant axial

1/n

ε

˙

strain rates between 102 and 105 s1. Test data

τ* (p, ε, T) = [c (T) + b (T)p]  

˙

(25)

i

corresponding to the strain rate εo ≈ 5 10-3 s-1

 εo 

˙

were selected in the following analysis to evalu-

when p = 0 (pure shear)

ate the strength parameters of ice. This strain rate

was defined by the authors of this report as the

1/n

ε

˙

instantaneous strain rate because the test strength

τ* (ε, T) = c (ε, T ) = c (T )  

magnitudes at this rate reached their maximum

values. The tests were carried out at four different

Accordingly

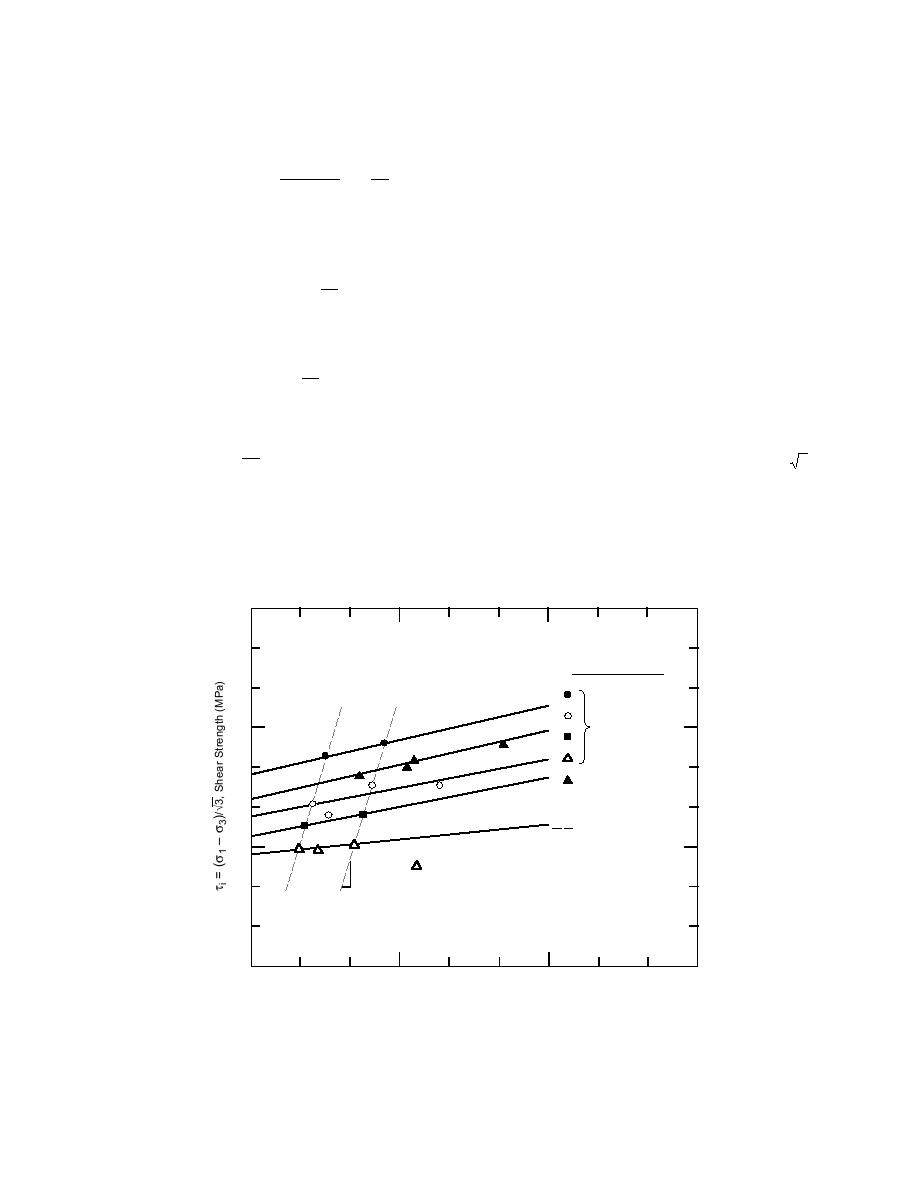
confining pressures: 1.38, 3.45, 6.89 and 13.79 MPa.

1/n

The test data replotted by the authors of this re-

ε

˙

port in terms of the shear strength τ i = (σ1 - σ 3 )/ 3

b (ε, T) = b(T ) 

˙

(25a)

 εo 

˙

vs. the hydrostatic pressure p = (σ1 + σ 2 + σ 3 )/3

are presented in Figure 3. Note that each point in

where parameters c(T) and b(T) are correspond-

ing to the strain rate ε = εo .

Figure 3 represents the mean of five tests.

˙˙

In Figure 3 for comparison tests, data are pre-

If the radial strain rates are taken into account

function Φ(ε) in eq 24, 25 and 26 should be re-

sented on triaxial compression of freshwater poly-

˙

placed by function Φ( γ).

crystalline ice obtained by Jones (1982). The ran-

˙

18

σ1 = 3

σ2 = σ3

.

ε1 ≈ 5100 s1 1

13 3 s

=5

σ3 = 1.38 MPa

σ3 = 6.89 MPa

16C

Labrador Ice

11.8

12

(data from

Gagnon and

Gammon, 1995)

11

6

Polycrystalline Ice

(data from Jones,

1982)

1

σ3 Trajectory

6

√3

0

15

30

45

p , Hydrostatic Pressure (MPa)

Figure 3. Strength test data of ice under triaxial compression. Data from Gagnon

and Gammon (1995) and Jones (1982).

7