Figure 1. Strength envelopes of ice at various temperatures

Ice Strength as a Function of Hydrostatic Pressure and Temperature

STRAIN RATE EFFECT

CR97_06
Page Navigation
2

in which the temperature variations of the ice

In the model of Fish (1991, 1992, 1993) the rela-

strength are characterized by only one param-

tionship

eter--the activation energy. The apparent activa-

τ * = τ * (p, γ i ) ;

T = Const

(1b)

tion energy magnitudes were found as E = 69 kJ

mol1 in the temperature range between 20 and

was described by a product of two functions: 1) a

40C (Rist and Murrell 1994), and E = 101 kJ

parabolic function--extended by Fish (1991) the

mol1 in the temperature range between 1 and

Drucker-Prager yield criterion, and 2) a normal-

16C (Gagnon and Gammon 1995). The higher

ized (dimensionless) power function of the strain

activation energy magnitudes were explained by

rate. The yield criterion describes the strength

grain-boundary softening associated with the pres-

dependency of ice on the hydrostatic pressure by

ence of liquid on grain boundaries.

means of three parameters: the cohesion c, the

Equation 1c implies that the nonlinear (with

friction angle φ and the magnitude of the hydro-

regard to stress) viscosity coefficient of ice,

static pressure σmax, at which the shear strength

of ice reaches a maximum τmax, related to the ice

η(T) = 1/B exp(E/RT) ,

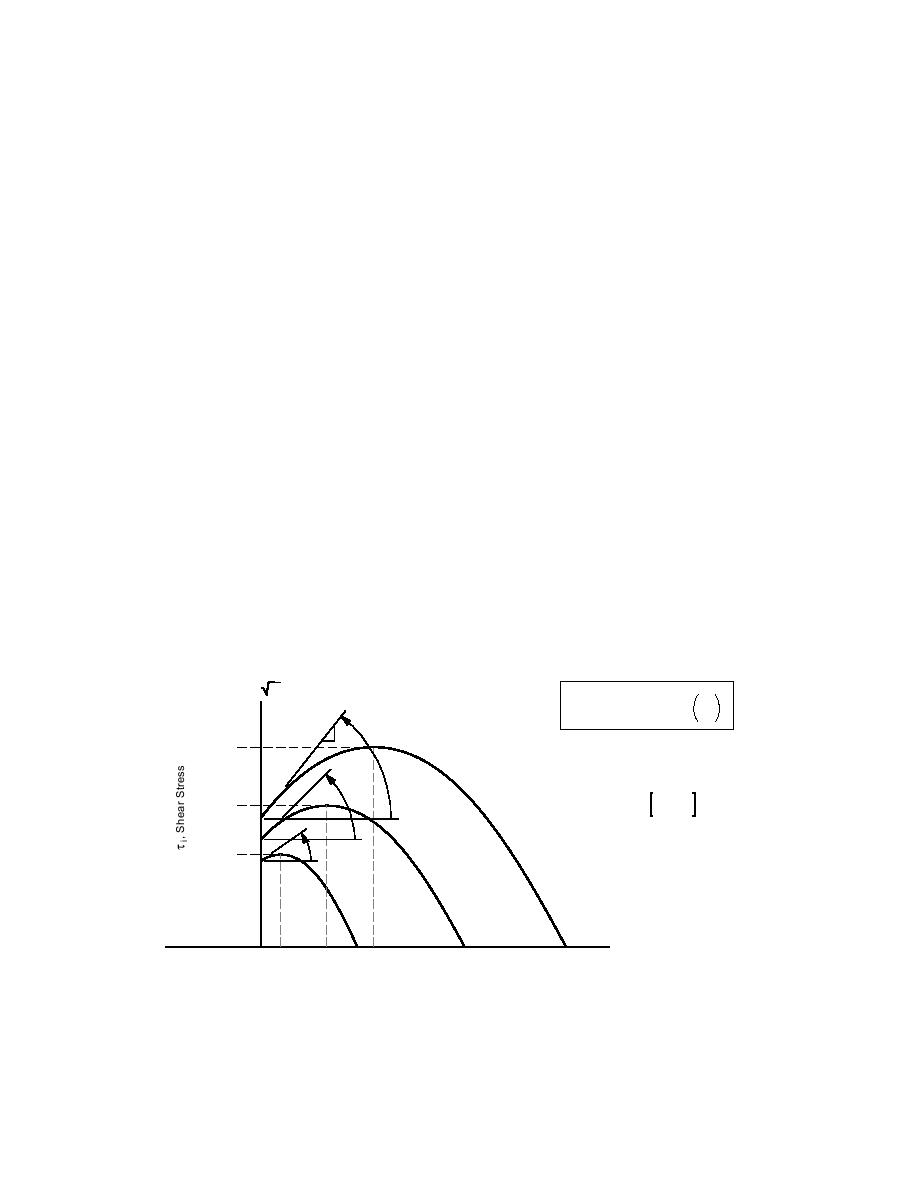
melting pressure p* (Fig. 1). The model described

Jones' (1982) test data well. It was shown that the

is independent of the hydrostatic pressure. In other

ice cohesion and the friction angle are functions

words, ice is assumed to be incompressible.

of the strain rate.

It has been shown earlier (Fish 1991) that the

The temperature effect on ice strength under

ice strength in a multiaxial stress state is charac-

triaxial compression was studied by Rist and

terized by two or more temperature-dependent

Murrell (1994) and Gagnon and Gammon (1995)

parameters that can affect the magnitude of the

using the Arrhenius-type (Norton-Glen) equation,

apparent activation energy: the ice cohesion, the

friction angle, and the hydrostatic pressure. So

ε = B exp(-E / RT ) τ n

(1c)

the predicted values of the ice strength, calcu-

lated by eq 1c, may deviate considerably from

where ε

axial (constant) strain rate

those obtained in the tests.

empirical parameter

A mathematical model (Zaretsky and Fish

activation energy

1996a, 1996b) takes into account the effect of all

universal gas constant

three variables in eq 1. The ice strength is de-

absolute temperature, K

scribed by three parameters: the ice cohesion, fric-

≈

4 = strain hardening parameter (Jones

tion angle and ice melting pressure. The ice cohe-

1982),

sion and the friction parameter are assumed to be

τi = J2

p 2

τ i = (c + bp) (c + bp*)

τ max 1

τ max = c + -- σmax

φ1

φ2

p*2 c

σmax = -- + p*

τ max 2

φ3

p* = p*(T); c = c(T)

τ max 3 c

b = b(T)

b(T) = tan φ(T)

0 σmax 3 σmax 2

σmax 1

p = , Hydrostatic Pressure

Figure 1. Strength envelopes of ice at various temperatures: c, φ, p*, and T are the ice cohesion,

friction angle, ice melting pressure, and absolute temperature, respectively.

Index

Privacy Statement
Press Release
Contact