b (T) = bo + b1 (T)
(19)
c*
a.
where bo = tan φo and φo is the angle of internal
friction of ice brought about at the time of ice
formation at 0C; b1(T) = tan φ1 (T), and φ1 (T) is
α(1
the angle of internal friction attributable to the
T/T
)
c(T) = c0 e
m
increased viscosity of the liquid phase (lubricant)
at grain boundaries at temperatures below 0C.
One may assume that the component b1(T) is
c0
proportional to bo and to the temperature melting
function, i.e.,
Tm
0
b1(T) = boβ (1 - T /Tm )
(20)
T, Temperature (K)
a. Ice cohesion, c(T).
where β is a parameter. Combining eq 19 and 20
[
]
b (T) = bo 1 + β (1 - T /Tm ) .
(21)
b*
b.
To simplify the parameter evaluation procedure,
ν
β(1
T/T
)
b (T) = b 0 e
eq 21 can approximately be presented in the form
m
b (T) = boe β (1-T /Tm )
ν
(22)
or
ν
b0
b (θ) = bo e β1 θ
(22a)
ν
where β1 = β /Tm . It was found that ν = 1/2 is in
Tm
0
agreement with test data.
At freezing when
T, Temperature (K)
b. Friction parameter b(T).
T = Tm = 273.1K (0C) ; b(0) = bo
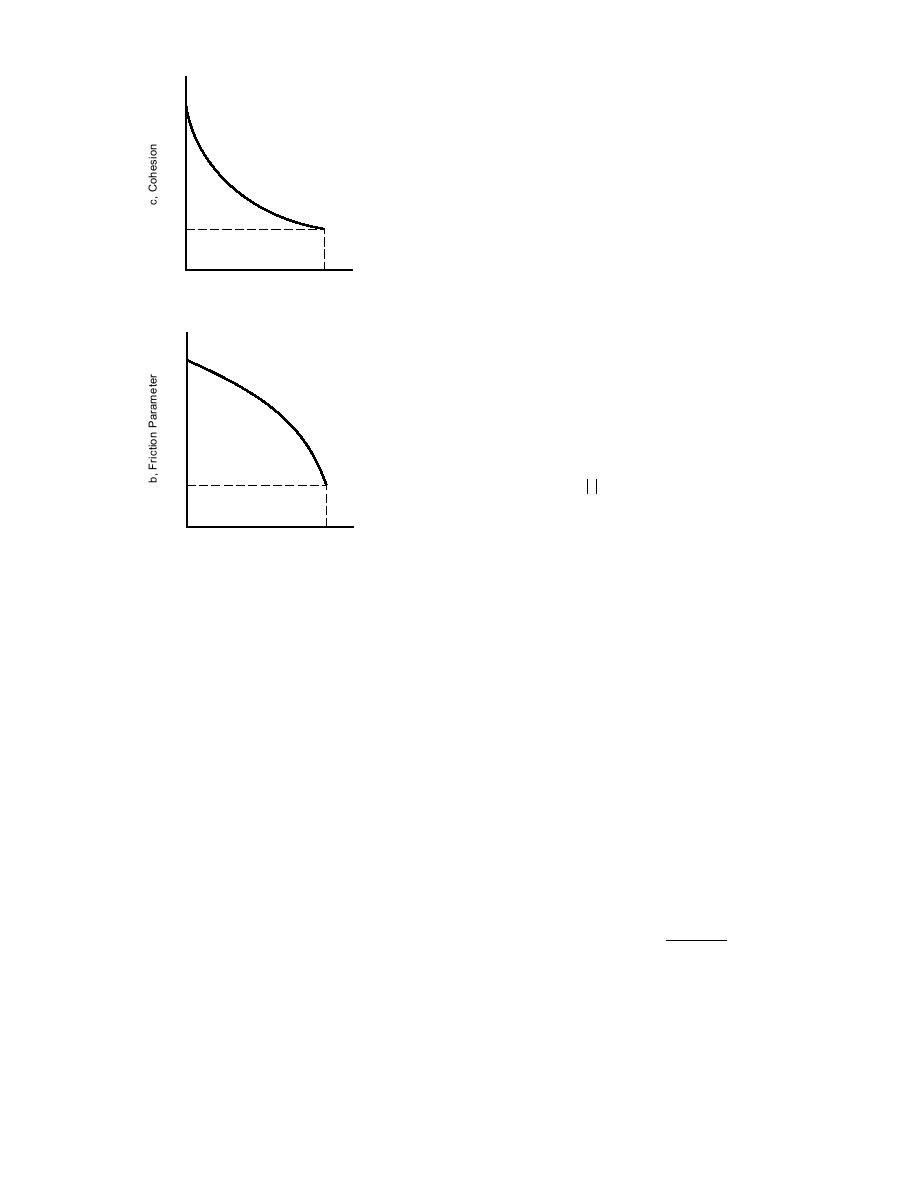
Figure 2. Temperature diagrams of the
at the absolute zero
strength parameters of ice.
T = 0 (-273.1C) ; b* = boeβ
described by
The temperature diagram of parameter b(T) is
c (T) = coeα(1-T /Tm )
(18)
given in Figure 2b. Note that at very low tem-
or
peratures certain adjustments of eq 15 through 22
c (θ) = coeα|θ|/Tm
(18a)
will probably be required.
in which = 1 and θ= (Tm T ) is ice tempera-
ture (C).
TEMPERATURE CRITERIA
Equations 18 and 18a can be considered ap-
OF ICE STRENGTH
proximate forms of eq 17. Note that at freezing
Since temperature dependencies of the ice
T = Tm = 273.1K (0C) ; c (0) = co
strength parameters have been established, eq 1d
when
taking into account eq 5 can be presented in an
explicit form
T = 0 (-273.1C) ; c* = coeα .
b(T)
τ io(p, T) = c (T) + b (T) p -
p2
(23)
2σmax (T)
The temperature diagram of parameter c is shown
in Figure 2a.
in which c(T), b(T) and σmax(T) are given by eq 7
Angle of internal friction
and 14 through eq 22a. Equation 23 is a tempera-
The parameter of internal friction of ice b(T)
ture criterion of ice strength in a multiaxial stress
can also be presented as a sum of two components:
state. To take into account the strain rate effect, eq
6




 Previous Page
Previous Page
