Figure 39. Construction elements of the Darnell tire model. (After Darnell et al. 1997.)

Rigid tire model

Table 7. Bending stiffness of tire sections

TR-01-16
Page Navigation
34

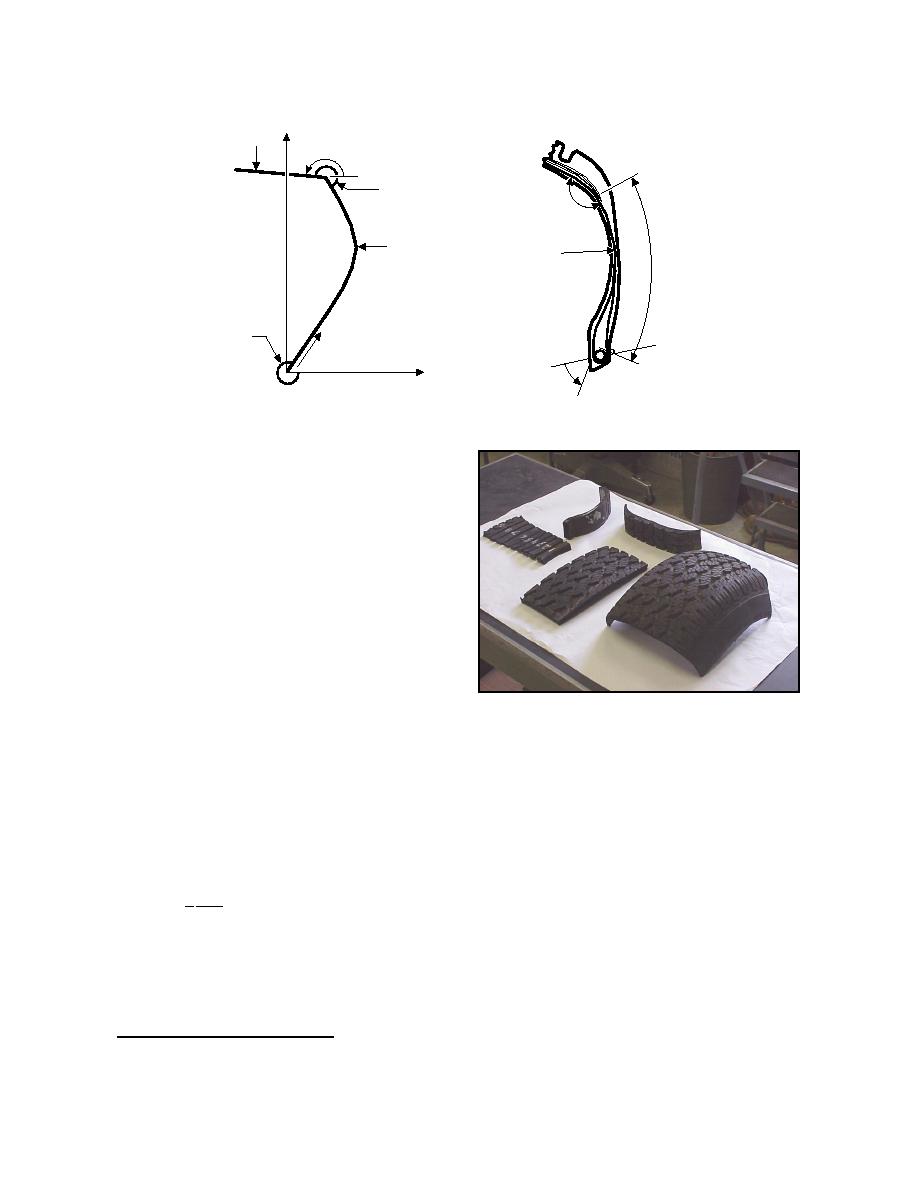
Figure 39. Construction elements of the Darnell tire model. (After Darnell et al. 1997.)

The Darnell tire model was validated for a Ford

Taurus tire for lateral forces and deflection on a

smooth surface and while rolling over an angled ver-

tical step (Darnell et al. 1997) and for slip angle and

aligning moment.* The model results sufficiently

mimic tire behavior while being computationally

efficient, indicating its potential for simulations of a

tire on deformable terrain. Some alteration in the

sidewall model may be necessary to account for the

interaction of the sidewall with the deformable terrain

if sinkage is substantial.

The same tire used to gather motion resistance

data on various terrain (snow, freezing and thawing

ground) was cut into four sections: sidewall, lateral

Figure 40. Cut tire sections used to determine

tread, longitudinal tread, and shoulder (Fig. 40). The

composite tire properties.

sidewall was further dissected into smaller sections

for future work expanding the sidewall model. The

sections were tested in the laboratory to determine

the beam stiffness (EI) by clamping an end of the test

section onto a workbench to form a cantilever beam.

Deflections were measured for a range of loads, and

stiffness was calculated using the equation for a can-

tilever beam with a point load on the free end:

1 Wl 3

ymax =

(25)

3 EI

where ymax = maximum deflection at the free end

of the beam

W = applied load

E = Young's modulus of the beam

* Personal communication with I. Darnell, University

of Michigan, 1997.

to contents

Index

Privacy Statement
Press Release
Contact