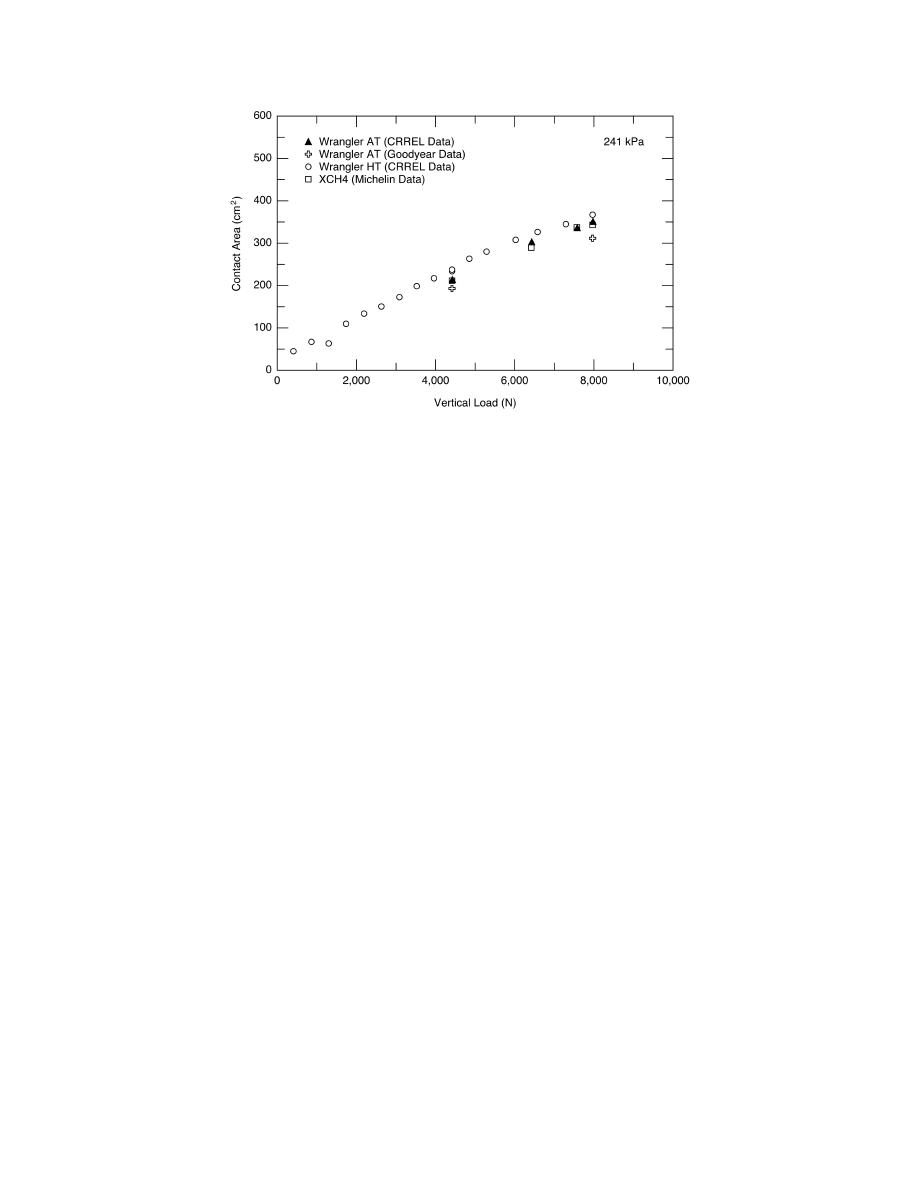
Figure 38. Comparison of measured contact area for the three test
tires at 241 kPa (35 psi).
Rigid tire model
ric analysis and refinement of the code (Alverez Sanz
1999).
If the deformable material is very soft, as in fresh
The objectives of the Darnell tire model are simi-
snow, the tire can be approximated as a rigid wheel.
lar to those needed for this study: an efficient, accu-
The rigid wheel is modeled as a rigid analytical sur-
rate, three-dimensional model to predict spindle
face 0.74 m in diameter and 0.272 m wide (for a full
(axle) forces but not the internal stresses in the tire.
wheel), with a 0.051-m radius of curvature on the tire
The contact forces are calculated in the process, so
shoulder. An unsprung mass of 636 kg is placed at
the model is also suitable for efficient modeling of
the axle to simulate the weight of the tire and the load
the tireterrain interaction, where accurate modeling
of the vehicle on the tire (6240 N); the rotational
inertia of the wheel was set to 2.15 kg m2.
of the contact stress distribution is imperative.
The tire is simulated with three modeling ele-
Darnell tire model
ments: the tread elements are six-degree-of-freedom
shell elements (S4R); the sidewall elements are three-
To adequately model the dynamics of a rolling
node, user-defined elements based on pre-calculated
tire, a very efficient tire model is needed. Thus, the
results from a sidewall model; and the contact is
tire model developed by Darnell and Hulbert at the
modeled using a "hard" contact, penalty method
University of Michigan is a promising alternative.
(HKS 1998). The roadway is modeled as a rigid sur-
The Darnell tire model (Darnell et al. 1997, Darnell,
face.
in progress) is an extension of a two-dimensional tire
The sidewall model is a special-purpose finite
modeling concept developed by Mousseau (Mous-
element code that generates a lookup table of side-
seau and Hulbert 1996) for interfacing with vehicle
wall forces (and geometry) using ten equal-length,
dynamics simulations. The tire is modeled using ma-
non-extensible beam elements with inflation pressure
terial properties for the composite material rather
as a follower load. The sidewall model is generated
than the individual components. The composite prop-
from the geometry of the uninflated sidewall, the
erties were obtained by sectioning the tire and per-
bending and shear stiffness for each element, and the
forming laboratory tests on each of the major section
tire inflation pressure. The results of the sidewall
components (tread, sidewall, and shoulder). A similar
model are implemented in the tire model through the
approach was also developed at the University of
user-defined element, which attaches to the tread
Birmingham in the UK for tire modal analysis (Burke
section with rotational springs (Fig. 39).
and Olatunbosun 1997a, 1997b, 1997c). Additional
work on the Darnell model has been toward paramet-
27



 Previous Page
Previous Page
