The constant-pressure entropy change due to changes in temperature of a pure
substance (eq 29) is calculated by
*
T2
Cp
T *
∆T2 Sm
=∫
dT .
(32)
T
1
T1
As with many solids, the heat capacity of H2O(cr,I) as a function of temperature
can be described by the MaierKelly (1932) equation:
c
Cp = a + bT +
.
(33)
2
T
*
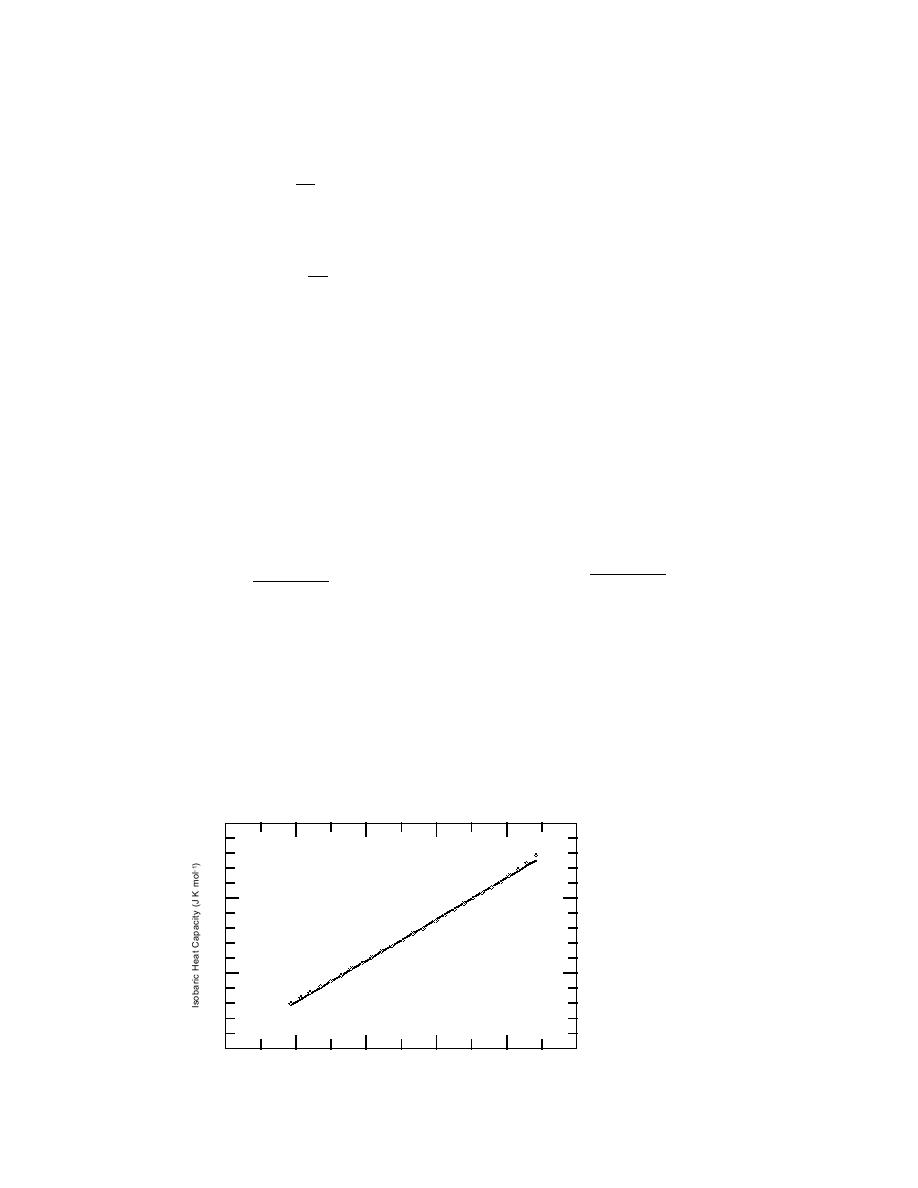
Values of Cp,H2O(cr,I) between T = 198.57 K and 268.39 K reported by Haida et al.
(1974) were fitted by nonlinear regression (Marquardt procedure) to eq 33 (SAS
Institute 1985). The data of Haida et al. (1974) and the fitted line are presented in
Figure 7. The regression had a coefficient of determination (R2) of 0.999 997. The
following parameter estimates (with parameter-estimate standard errors in paren-
theses) were obtained:
a = 10.6644 (1.5999) J K 1 mol 1
b = 0.1698 (0.0046) J K 2 mol 1
c = 198 148. (28 230.) J K mol 1 .
Equation 32 was calculated by
[
]
*
c
dT = a ln(Tf ) ln(Trw ) + b(Tf bTrw ) +
Tf
Cp,H 2O(cr,I)
(
)
∫
2 Tr2 Tf2 .
(34)
T
w
Trw
Molar entropies of electrolyte solutions
The procedure for calculating the molar entropies of electrolyte solutions can be
derived from equations found in standard texts on chemical thermodynamics (e.g.,
posed of nA moles of A (by convention, the solvent) and nB moles of B (again, by
convention, the solute) is
SM = SA + SB .
(35)
Figure 7. Constant-
40
pressure heat capacity
of H2O(cr,I) under p =
0.101325 MPa and T =
200 K to 268 K as re-
35
ported by Haida et al.
(1974). The line was
calculated by a regres-
sion fit of the data to
30
the
MaierKelly
model.
25
180
200
220
240
260
280
Temperature (K)
14




 Previous Page
Previous Page
