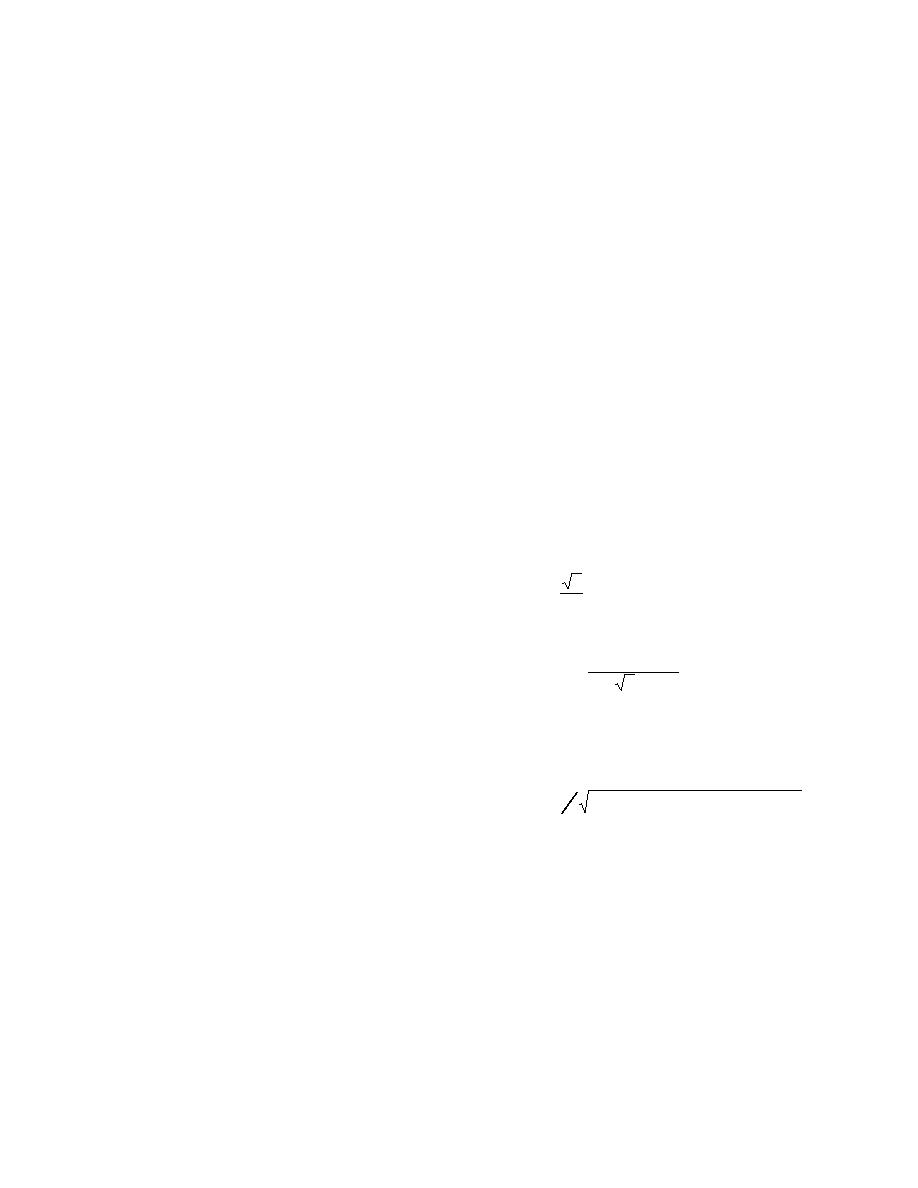
unit stress of 6.9 kPa (1.0 lb/in.2); Co, C1, and C2
The two other forms that were used to repre-
sent the unfrozen water content in the governing
are constants; S is the degree of saturation, in %;
So is a unit saturation, 1.0%; γd is dry density, in
parameter of eq 1 were directly related to the un-
Mg/m3; and γo is a unit density (1.0 Mg/m3). To
frozen water content, as follows: 1) wug, expressed
as a decimal, normalized to a unit unfrozen water
conduct the regression analysis, we linearized this
content, wo, of 1.0; and 2) the volumetric unfro-
equation to form
zen water content, wuv, expressed as a decimal,
ln Mr = A0 + A1 ln (S / S0 )
normalized to a unit unfrozen water content, wo,
of 1.0. The volumetric unfrozen water content was
+ A2 ln (γ d / γ o ) + A3 ln [ f (σ)] .
(9)
determined with
wu- v = wu-g γ d
(5)
For a particular set of conditions, then
where γd = dry density (Mg/m3). The resulting
K1 = e A0 (S / S0 )
(λ d / γ o ) A2
A1
and K2 = A3 .
equations with these terms substituted as the gov-
erning parameter were:
Three stress parameters were investigated to
help characterize the stress dependence of the ma-
(
)K
Mr = K1 wu-g / wo
2
terials tested. These included J1, the bulk stress
(or first stress invariant); τoct, the octahedral shear
Mr = K1(wu- v / wo )
K2
stress; and J2/τoct, the ratio of the second stress
.
invariant to the octahedral shear stress. In our re-
peated-load triaxial test, where σ2 = σ3 and σ1 =
In analyzing the frozen resilient modulus data,
the value of the governing parameter wu- g / wt ,
σ3 + σd, the functions are given as:
wu- g / wo , or wu- v / wo at each test point was de-
J1 = 3σ3 + σd
termined from the temperature (and total water
content, if necessary.) Then, regression analysis
2
was conducted to determine the relationship be-
τoct =
σd
tween these values and the measured resilient
3
modulus. Data from the thawed, undrained state
and
(assigned to be at a temperature just barely below
9σ32 + 6σ3σd
freezing) were analyzed along with the frozen data.
J2 / τoct =
2σd
Thawed/never frozen
where J1 = σ1 + σ2 + σ3
For the never frozen and thawed data, the gov-
erning parameter in the general form equation (eq
J2 = σ1σ2 + σ2σ3 + σ1σ3
1) was set to be a stress function. The constant K1
was considered to be a function of the moisture
level expressed as the degree of saturation in the
τoct = 12 (σ1 - σ2 )2 + (σ2 - σ3 )2 (σ1 - σ3 )2 .
sample and, when a range of data were available,
the dry density. Thus, the general equation be-
We found that the bulk stress parameter (J1) pro-
comes
vided the best fit to the data for the class 6 special
base material. The ratio J2/τoct was the stress pa-
Mr = K1[ f (σ)]K2 ,
(6)
rameter that best fit the data of the three subbases
class 3 special, class 4 special, and class 5 special,
which includes the term
and τoct best characterized the clay subgrades.
K1 = C0 (S / S0 )C1
(7)
We also analyzed the data from the class 6
special base material in the thawed condition us-
or
K1 = C0 (S / S0 )C1 (γ d / γ o )C2
ing an equation of the form
(8)
Mr = K1 e K2 [ f (σ)].
where f(σ) is a stress parameter normalized to a
(10)
9




 Previous Page
Previous Page
