had little effect. After deformation takes place, recov-
Mae and Higashi also analyzed separately changes
ery processes have been observed that restore the orig-
in the mobility and concentration of minority charge
inal conductivity if the total strain was small. Rapid
carriers caused by plastic deformation. They used for
and large deformation, however, causes permanent
this purpose their experimentally obtained frequency
dependencies of σ and ε, but exploited a theory
changes in the conductivity and dielectric permittivity.
Itagaki (1978, 1982, 1983) conducted a very inter-
by MacDonald (1953), which is not applicable to ice.
esting series of experiments and theoretical calcula-
Their results showed unrealistic magnitudes for an
ion mobility of 0.6 cm2/V s. Nevertheless, when the
tions aimed at determining the contribution of electri-
cally charged dislocations to the electrical properties
same experimental technique is combined with a spe-
of ice. In 1978 he carried out an exciting experiment in
cific theory for ice (Petrenko and Ryzhkin 1984a),
which he compared the electrical properties of disloca-
it gives a correct value for mobility of ions, of a few
103 cm2/V s (Zaretskii 1991).
tion-free areas of ice pure microcrystals with areas
having a high density of dislocations. He used hoar-
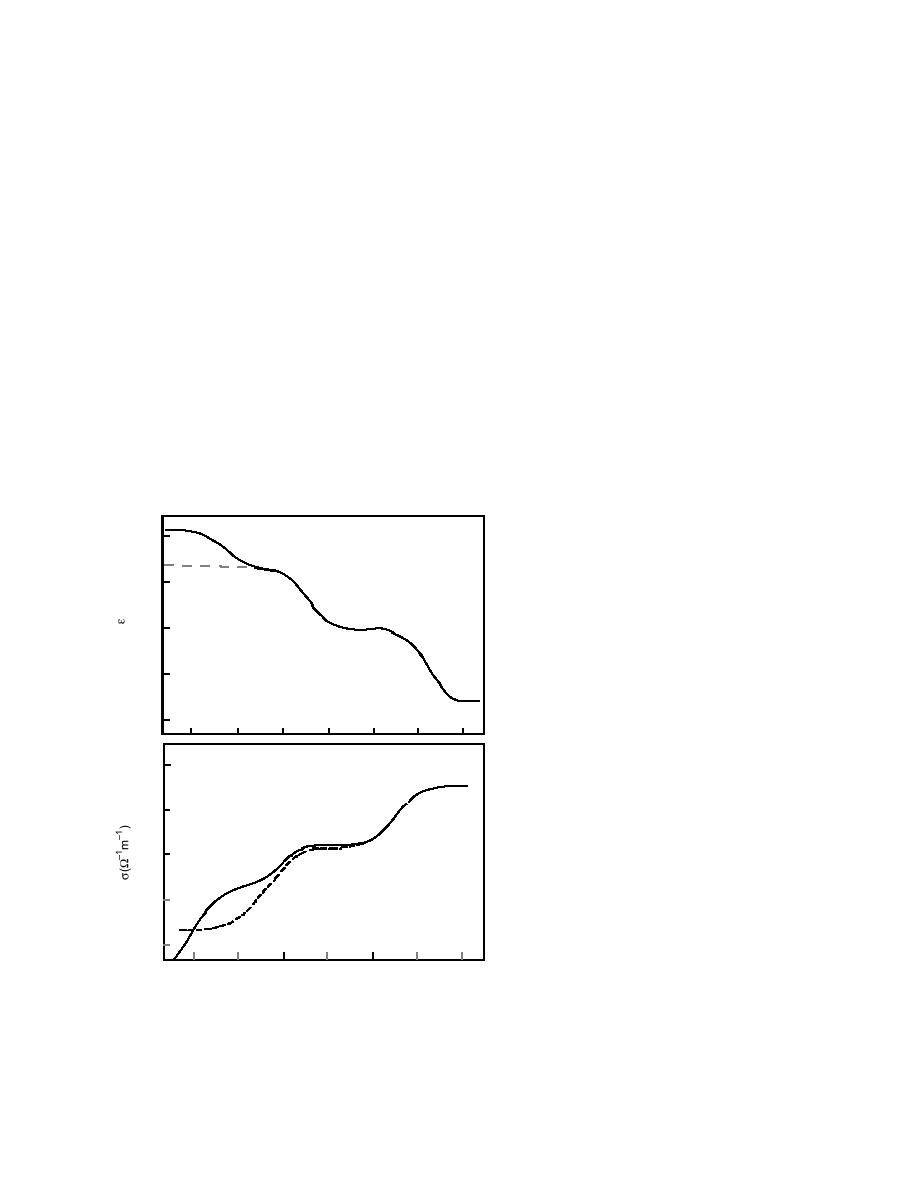
Noll (1978) studied the influence of plastic defor-
frost crystals as the specimens and X-ray topography
mation on electrical properties during and after defor-
mation. He measured σ and ε at T = 3 and 10C in a
to visualize dislocations in them. Use of tiny liquid-
mercury electrodes prevented damage to the ice crys-
from 2 105 to 103 s1, and a strain range from 0.03
tals. Itagaki did not observe the Debye dispersion of σ
and ε in dislocation-free regions, while it was present
to 0.6. He found that plastic deformation reduces the
electrical conductivity in the space-charge dispersion
in the regions with high dislocation density and in the
frequency range (Fig. 38). The decrease depended
initially dislocation-free regions after introduction of
strongly on the strain rate, while the strain magnitude
dislocations by surface scratching. On the basis of
these observations, he concluded that the main reasons
known for the polarization process in ice, the De-
bye dispersion and hence the high-frequency con-
10000
ductivity σ∞, are related to the motion of charged
dislocations in an ac electrical field.
1000
He later developed a theoretical model support-
ing this idea (Itagaki 1982, 1983). However, Ita-
gaki's model was not accepted by the ice physics
100
community. While dislocations in ice can contrib-
D
ute to and modify the electrical properties of ice,
they cannot account completely for those electri-
10
cal properties. There may be other reasons for the
absence of Debye dispersion found by Itagaki in
1
very thin and pure specimens of ice. One possibil-
ity is that the specimen thickness was comparable
with or less than a screening length. Conventional
10 4
theories of electrical properties of ice (Jaccard
1964) predict an absence of the Debye dispersion
D
10 5
in this case (Petrenko and Ryzhkin 1984a).
10 6
LITERATURE CITED
Alexander, H. and H. Teichler (1991) Disloca-
10 7
tions. Materials Science and Technology, 4: 249
301.
10 8
Barer, S.S., V.I. Kvlividze, A.B. Kurzaev, V.D.
Sobolev and N.V. Churaev (1977) Thickness and
0.1
1
10
100
1kHz
10kHz
100kHz
viscosity of thin unfrozen layers between ice and
f (Hz)
quartz surfaces. Doklady Akademii Nauk USSR,
Figure 38. Effect of plastic deformation on dielectric per-
235(3): 601603.
Barnes, P., D. Tabor and J.C.F. Walker (1971)
were obtained before deformation, dashed lines were obtained
during plastic deformation at ε p = 3.2 105 s and εp = 0.274.
˙
ceedings, Royal Society, A325: 127155.
T = 270.2 K.
27




 Previous Page
Previous Page
