to sliding velocity. Thus
11 m/s
2.2
dQ
ds
I=
=λ
∝v
(2)
dt
dt
1.6
8.3 m/s
where Q = electrical charge
λ = surface charge density that the slider
1.0
picked up from the ice surface
s = area swept
0.4
5.5 m/s
v = sliding velocity
t = time.
-0.2
When the input impedance of a measuring device is
160
480
800
1120
1440
much larger than the resistance of ice R, the charge
Time (s)
generated flows through the ice, resulting in a potential
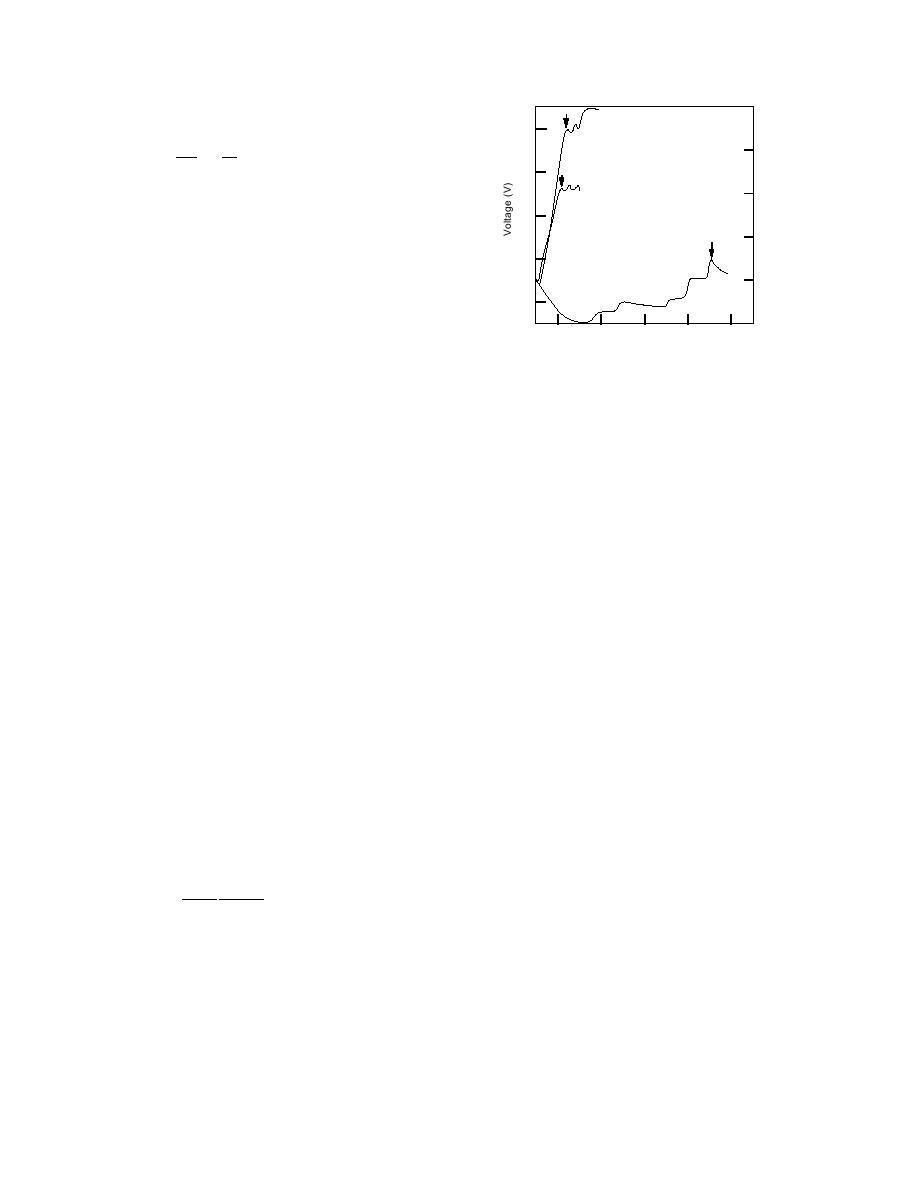
Figure 7. Records of the potential difference V
difference V
across a capacitor built into a ski at three slid-
ing velocities (after Petrenko and Colbeck 1994).
V = IR .
(3)
Temperature was 4C. Skier started at t = 0 and
slowed at the moments marked with the arrows.
Since R for ice increases exponentially with de-
creasing temperature (see the Electrical Properties of
Ice [Petrenko 1993b]), the observed electrification ris-
acter of the electrification observed in the field experi-
es rapidly at low temperatures. The charge density
ments agrees well with the laboratory results. One of
λ found at T = 10C was about 1.6 106 C/m2 and
the most noticeable differences is that, in the field, V
105 C/m2 at 35C. An even higher charge density
first becomes negative and only then positive. At the
of about 104 C/m2 accumulated at the ice/dielectric
highest speed, V reached 2.2 V, which corresponds to
λ = 3.6 107 C/m2. This charge density was compara-
slider interface. Since it is unlikely that a slider picks
up all the surface charge from the ice, these values of λ
ble with a value of 1.6 106 C/m2 found on ice. In the
absence of the buffer capacitor C, V would have been
appear to be a lower limit.
At temperatures below 10C, the density of charge
4.4 103 V if there had been no electrical breakdown
collected from the surface becomes nonlinearly depen-
of the air or the ski dielectric material. And this is not
dent on the sliding velocity (see Fig. 6). While at T =
yet at saturation. According to the laboratory results,
10C, I is proportional to v, at 14C I increases as
we can expect even higher voltages at lower tempera-
v1.5 and at T = 25C it increases as v2.
tures. A reader interested in ski electrification can find
In the field experiments, we used an alpine ski as a
more details in Colbeck's (1994) publication.
slider on snow (Fig. 1). The ski itself acted as a flat
Possible reasons for electrification by friction, i.e.,
capacitor C0 to measure an electrical field of strength E
the accumulation of the electrical charges transferred
generated by charge density λski that accumulated on
from the ice surface onto the slider, can be classified
the bottom ski surface. A larger capacitor C = 2 F,
into two categories:
connected in parallel with C0, reduced the potential
1. The slider sweeps up the charge already present
difference V to a magnitude that could be measured by
at the ice surface.
a portable data logger carried by the skier in a back-
2. Friction somehow produces a spatial separation
pack. It is easy to show that
of the charge, which is then swept up by the slider.
After analyzing our data and the known ice surface
λski d C0
V=
properties, we favor mechanism 1. Figure 8 shows a
(4)
2ε0ε C + C0
very general electrical charge distribution in ice near
the surface. In a thin subsurface layer, a charge layer of
an extremely high density λs is formed. The major fac-
where ε0 and ε are the dielectric permittivities of a vac-
uum and of the material between the metal plates in the
tor leading to its formation is the ordering of dipole
ski respectively. The reduction factor C0/(C + C0) was
moments of the water molecules in the upper mono-
5.1 104.
The field measurements of snow frictional electrifi-
ordering was initially suggested by Weyl (1951) for
cation were made in deep powder snow in British
water and was later used by Fletcher in his model of
Columbia. Figure 7 shows a typical record of V taken
the ice surface structure. Other evidence for the exist-
at 4C at three different velocities. The general char-
ence of such an ordered layer of water molecules at the
5




 Previous Page
Previous Page
