Static equilibrium in the film perpendicular to the par-
ticle surface requires that the particle must exert a body
force per unit volume, g, equal to
(PL - Po )
g=
(78)
.
y
If the film is not of a uniform thickness, the body
force will drive tangential fluid flow to return the film
to a uniform thickness. Using equilibrium thermody-
namics, Gilpin (1979) then derived the following
expression for the thickness of the film (h) as a func-
tion of temperature, pressure, and surface curvature:
-
(Vs - VL )PLh + VsΨSL K - Lf TL T To = ah-α
~
(79)
where PLh is the difference between the pressure in the
film at the ice/water interface and the reference pres-
sure. Using this model along with experimental results,
Gilpin (1979) concluded that the value of α is approx-
imately 2.
Gilpin (1980) used an approach similar to Miller's
in developing a model to predict frost heave in soils,
although his model was simpler due to his initial approx-
imations. His model includes the model of the pressure
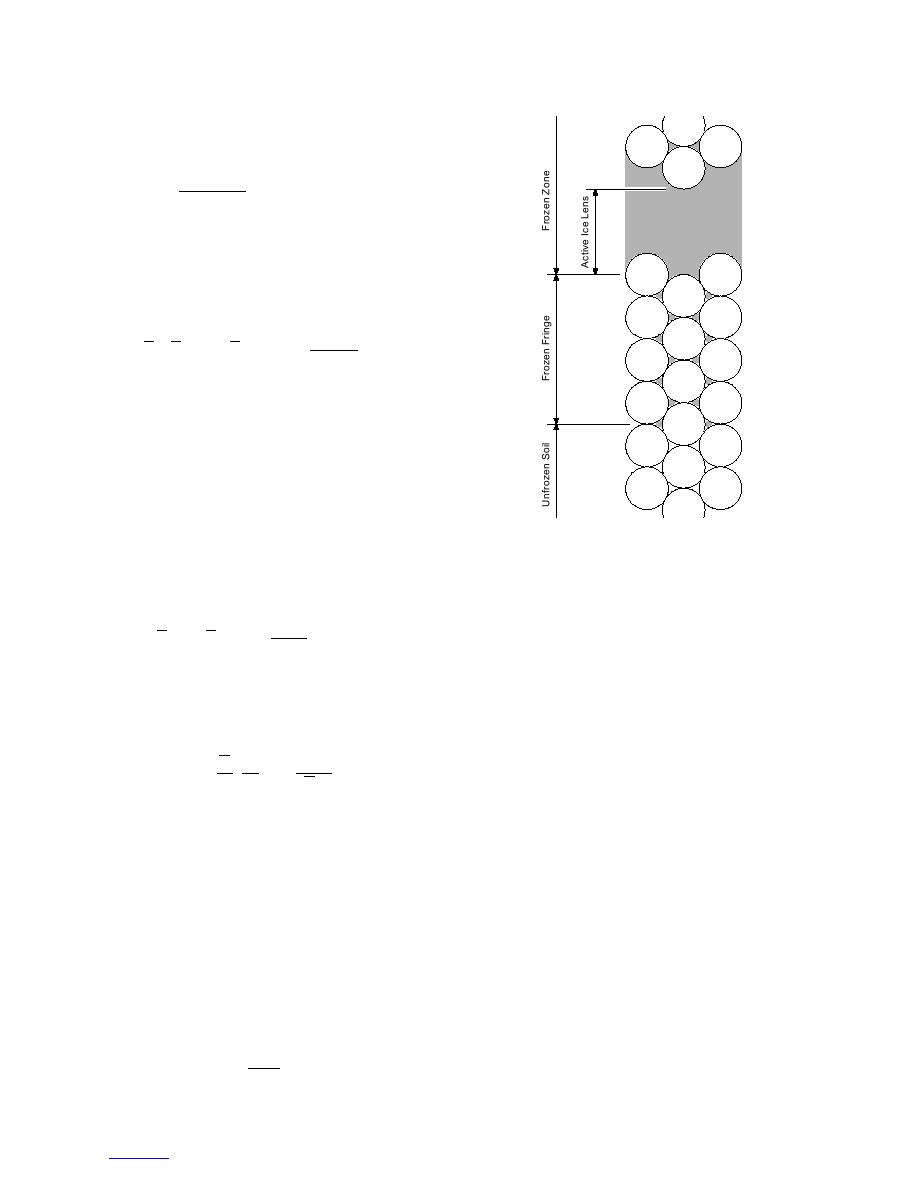
Figure 11. Gilpin's idealized model
gradient in the water near a solid/liquid interface
of the frozen fringe in a matrix of
described above. This is similar to the use of osmotic
uniform spheres. (After Gilpin
pressure as described by Loch (1978). Gilpin's model
1980.)
is also based on the GCE:
~ L ∆T .
Vs PLh - VsΨSL K = f
(80)
He estimated the hydraulic conductivity of the frozen
VsT
fringe based on simplifying assumptions regarding the
Assuming that Darcy's law is valid, Gilpin derived
packing of uniform spheres (Gilpin 1980). Figure 11 is
the relationship between driving potential tangential to
Gilpin's idealized model of a frozen fringe in a matrix
soil particle surfaces and flow rate of water in the con-
of uniform spheres, showing a graph of the tempera-
tinuous liquid phase. The equation that resulted is
ture and pressure gradients.
Gilpin (1980) developed numerical solutions to his
V
L ∆T
vw = - K s Ps + f
mathematical model of frost heave for a 100-mm col-
(81)
g z
VsT
umn. The "soil" was a matrix of 2-m uniform spheres.
A constant subfreezing temperature was imposed on
where Ps is the pressure of the ice phase. Thus (like the
the top surface, and a temperature slightly above freez-
rigid ice model) the flow rate is governed by the ice
ing was imposed on the bottom surface. Gilpin's results
pressure gradient, temperature gradient, and hydraulic
are qualitatively and quantitatively similar to those
conductivity in the frozen fringe. Gilpin assumed that
reported in O'Neill and Miller (1985).
the pore ice formed a continuous three-dimensional
network, but that it remained stationary. To address the
Summary of the thermodynamic
question of ice lens formation, he used relations among
formulations of frost heave
interface curvature, pressure, and temperature to estimate
Taber (1929) proved that frost heave was not caused
the ice pressure at which the force of contact between
by the volume expansion of water upon freezing, and
two particles will drop to zero. For most situations of
introduced the idea that frost heave was dependent on
interest, this ice pressure is equal to the overburden
freezing rate and occurred in a direction perpendicular
pressure, POB, plus the pressure difference across the
to heat flow. Beskow (1935) contributed the important
ice/water interface:
idea that frost heave is analogous to soil drying and
2ψ sl
PSEP = POB +
that in fine-grained soils frost heave is sometimes lim-
(82)
.
R
ited by water flow in the soils. He also noted that in-
16




 Previous Page
Previous Page
