terms, thus coupling models of heat and mass transport
ydraulic resistivity influencing frost heave rate (Miller
in freezing soils. Note that the volumetric ice flux in
1972).
soil, described by eq 71, consists of the volumetric ice
To complete his model, Miller (1978) applied the
content (a function of φ) times the rate of frost heave.
conservation of mass and energy in the frozen fringe,
The volumetric ice content can change within the frozen
along with the relations already mentioned, to obtain
fringe because of temperature effects as reflected in the
the relations among frost penetration rate, rate of frost
φ value.
heave, and rate of heat loss. Miller's rigid ice model
Frost heave that occurs once a frozen fringe is formed
was put into finite element form; some results are
is referred to as secondary heaving, while frost heave
reported in O'Neill and Miller (1985). Equations of the
with no frozen fringe is primary heaving (assuming an
model were solved for one-dimensional freezing of an
adequate water supply). With primary heaving, only the
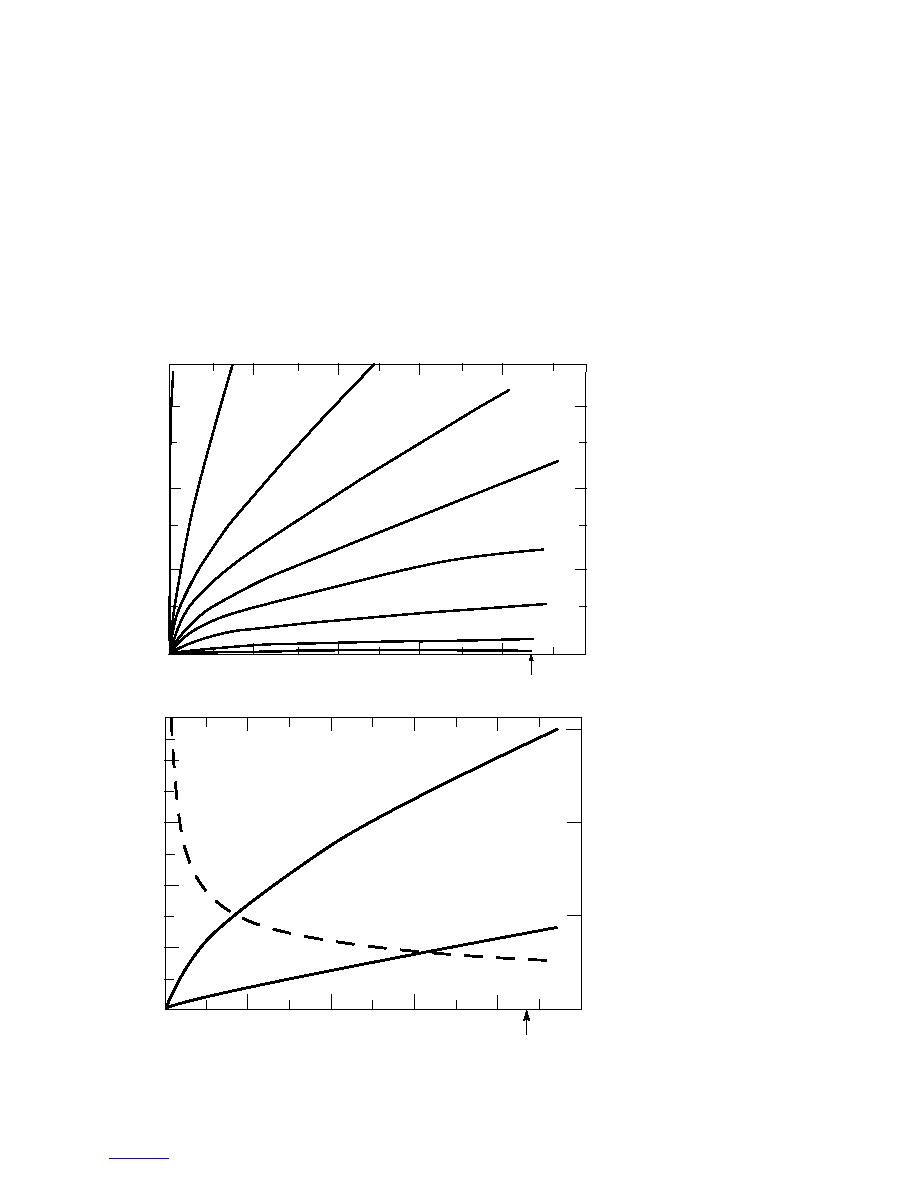
initially unfrozen, saturated soil column. A 153-mm soil
rate of heat loss controls the rate of frost heave, while
column of silt with a given function of unsaturated
with secondary heaving, there is a component of
hydraulic conductivity vs. liquid water content was
50.1
90.3
96.9
100.3
3
kPa
103.6
2
h
(mm)
a. Cumulative frost heave as a
107.0
function of time for various val-
1
ues of overburden pressure.
112.8
125.4
150.4
0
6
0
0.2
0.4
0.6
0.8
1.0 x 10
† (s)
10 Days
1.5
Large Scale
4
h
3
1.0
h
VI
hw
(mm/day)
h
(cm)
2
0.5
hw
VI
b. Heave rate (vI), cumula-
1
tive heave (h), and heave
due to water intake (hw) as
a function of time.
0
0
10 X 106
0
2
4
6
8
† (s)
100 days
Figure 9. Typical results of Miller's rigid ice model of frost heave, reported by O'Neill and Miller (1985), for a
saturated silty soil.
14




 Previous Page
Previous Page
