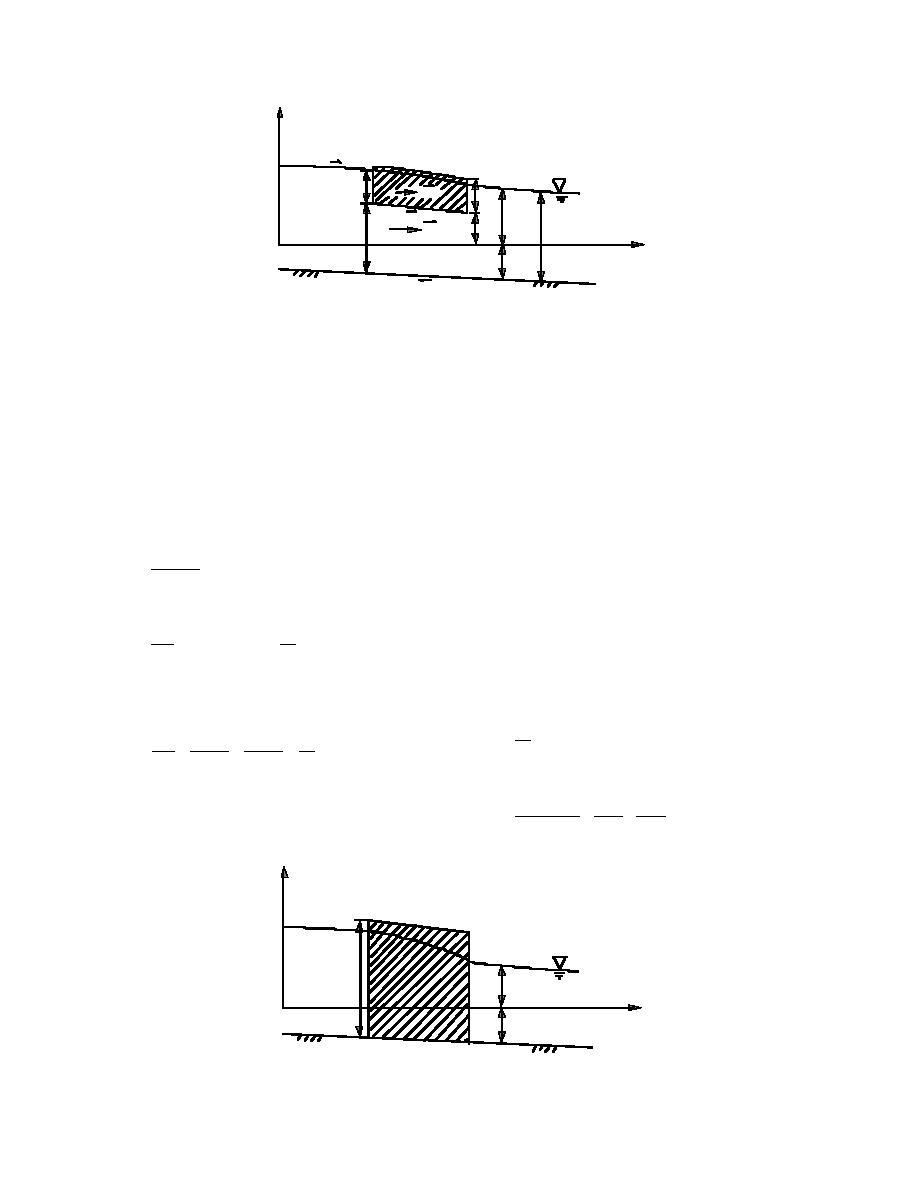
z
τs
ti'
qu
ti
τs
η
η'
x,y
ql
H'
H
h
τb
Figure 3. Definition sketch.
qtx = qlx + qux, qty = qly + quy = components
fraction of the solid phase in the icewater
mixture
of total unit width water discharge
→
q1 =
qlx, qly = components of the unit-width water
unit-width water discharge beneath the
discharge beneath the ice layer
ice layer
→
q =
qux = qix + qsx, quy = qiy + qsy = water discharge
unit-width water discharge in the ice layer
→u
→
Vi Nti = unit-width ice discharge
in the upper ice layer
q ice=
→
qix = Vix(η η′)(1 N) and qiy = Viy(η η′)(1
Vi =
ice velocity.
N) = water discharge carried by ice
Vix, Viy = ice velocity
Since the ice mass conservation gives
qsx, qsy = components of unit-width water discharge
[ρiti N ]
→
= -∇ ⋅ (ρi q ice )
in the ice layer relative to the moving ice
t
or the seepage discharge in stationary ice
accumulations.
eq 1 reduces to
When the surface ice is grounded, whether it is
→→
H
(
)
+ ∇ ⋅ ( q l + q u ) = ( Nti′) .
(2)
moving or stationary, the condition η - η′ = ρi / ρ ti
t
t
is no longer valid, and the lower layer discharge ql is
Therefore, the continuity equation for the total water
zero. In this case, as shown in Figure 4, the water mass
discharge is
conservation equation becomes
→
[(1 - N )∆η] = -∇ ⋅ q u
(4)
(qty )
H
(qtx )
+
+
= ( Nti′)
t
(3)
t
x
y
t
in which, ∆η = H. Equation 4 can be rewritten as
where
H (1 - N )
qty
(5)
qtx
+
+
=0
H = h+ η = total water depth
t
x
y
η = water surface elevation
and qlx, qly = 0.
z
ti
η
Ice
x,y
h
Figure 4. Definition sketch for grounded ice accumulation.
4



 Previous Page
Previous Page
