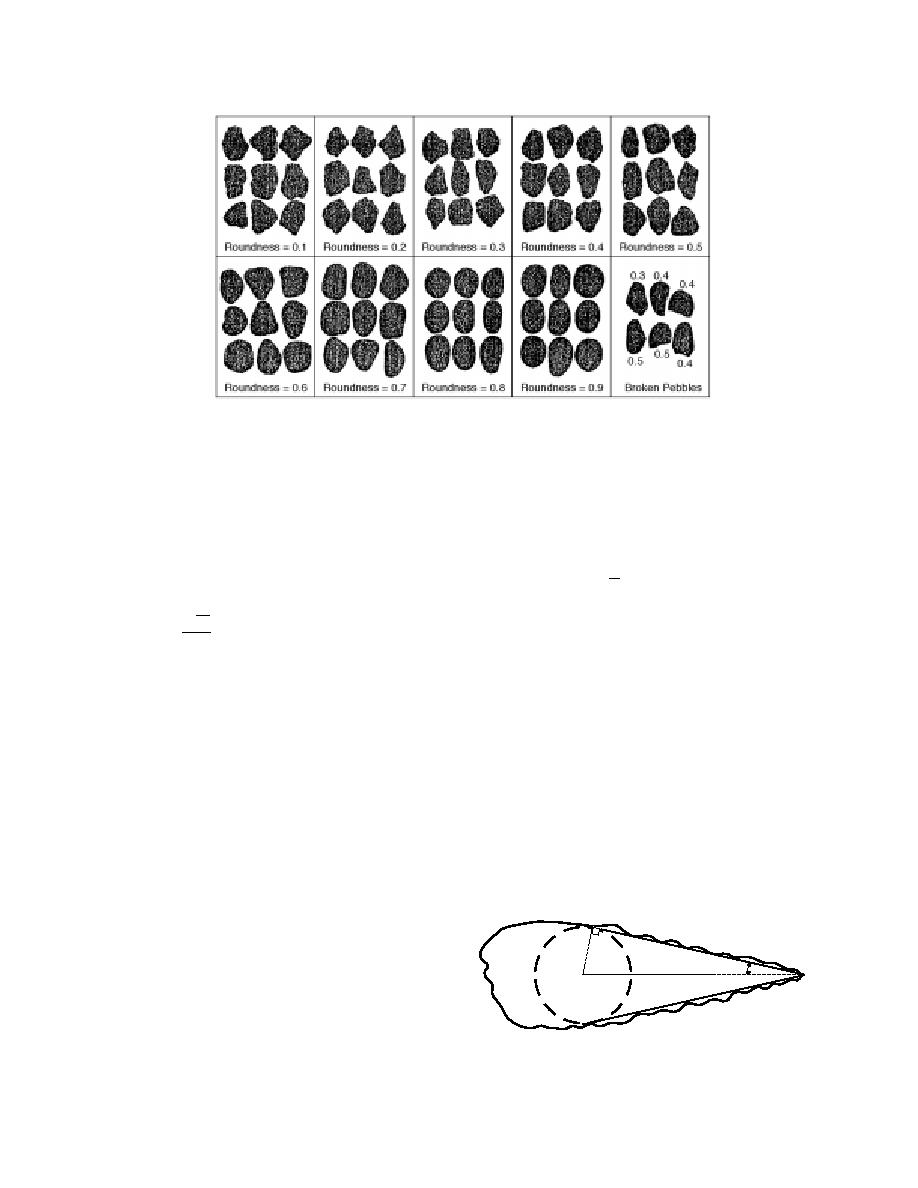
Figure 2. Roundness chart for 16- to 32-mm aggregates. (After Krumbein 1941.)
crushed aggregates. Lees (1964) proposed a meth-
the edges and corners of the particles also are
od for determining the degree of angularity, which
determined. These radii are used to index the
accounts not only for the roundness of the corner
roundness of the aggregate as shown below.
but also how far the projection is from the in-
Details on this method can be found in the papers
scribed circle (Fig. 3). The degree of angularity is
by Wadell (1932) and Krumbein (1941). Essen-
calculated by the following equation:
tially, the roundness (R) of a particle is an average
measure of curvature of the corners and edges. R
x
Ai = (180 a)
is expressed as
r
r
where Ai = degree of angularity
∑
R = r′
a = measured angle
N
x = distance to the tip of the corner from
the center of the maximum inscribed
where r = radius of curvature of a corner of the
circle
particle surface
r = radius of the maximum inscribed circle.
r′ = radius of the maximum inscribed cir-
cle in the projected plane
The total degree of angularity (A) is the sum of all
N = number of corners.
the values for all corners measured in three mutu-
ally perpendicular planes. Again, because of the
Because this is a lengthy process, visual charts
high degree of complexity, Lees (1964) developed a
have been developed (Krumbein 1941) for esti-
visual chart for determining the degree of angular-
mating the roundness of aggregates. Figure 2 can
ity of particles (Fig. 4).
be used to classify the roundness for 16- to 32-mm
ASTM D 2488-90 (1996), Standard Practice for De-
aggregates. By enlarging or reducing the chart,
scription and Identification of Soils (Visual-Manual
similar roundness charts could be made for other
Procedure), describes the angularity of coarse-
size aggregates (Krumbein 1941). The roundness
grained material as either angular, subangular,
(R) varies between 0.1 and 0.9. An R value greater
than 0.6 indicates high roundness, R between 0.4
and 0.6 indicates medium roundness, and R less
than 0.4, low roundness.
r
α/2
x
Description of angularity
Inscribed
Lees (1964) found that when using Krumbein's
Circle
(1941) method for determining the roundness
Aggregate
number, it was possible to get the same round-
Figure 3. Parameters for determining the degree of
ness number for two very differently shaped
angularity. (After Lees 1964.)
aggregates. He found to it to be especially true for
3



 Previous Page
Previous Page
