ICE PROPERTIES USED IN HYDRAULIC MODELS OF ICE JAMS

Figure 4. Typical breakup ice jam with equilibrium section

Roughness calculated from discharge measurements or estimates

CR99_11
Page Navigation
8

surface of the ice over time and as the ice cover

ICE PROPERTIES USED IN HYDRAULIC

thickens--effects noted by many observers--can

MODELS OF ICE JAMS

be a source of error in estimates of roughness,

The properties of ice jams included in the mod-

which is often taken as constant over time. Al-

els cited above include ice cover roughness, cohe-

though it has been argued by some that excessive

sion, measures of internal strength such as inter-

reliance is placed on this single work by

nal friction angle and the angles of static and

Nezhikhovskiy, a careful review of this work in-

dynamic friction, the shear force on the ice cover

dicates that both the method and the number of

and its shear strength, and frazil particle diameter

samples utilized by Nezhikhovskiy inspire confi-

and fall velocity. Each of these is addressed in a

dence. Rather, it is the incorrect application of re-

separate section below, followed by discussions

sults clearly intended by Nezhikhovskiy for use

of ice transport, thermal effects on ice jams, and

during initial ice cover formation due to frazil or

miscellaneous hydraulic properties of ice jams

sheet ice accumulation or frazil deposition only,

such as porosity, anchor ice growth, jam erosion,

to other situations, particularly breakup jams, that

engenders difficulty in roughness estimation.

ice cover breakup and movement, thermal effects,

Roughness is approached in several ways and

coefficient of ice loss, and permeability.

using several coefficients. Roughness is almost

always determined using a two-layer system, that

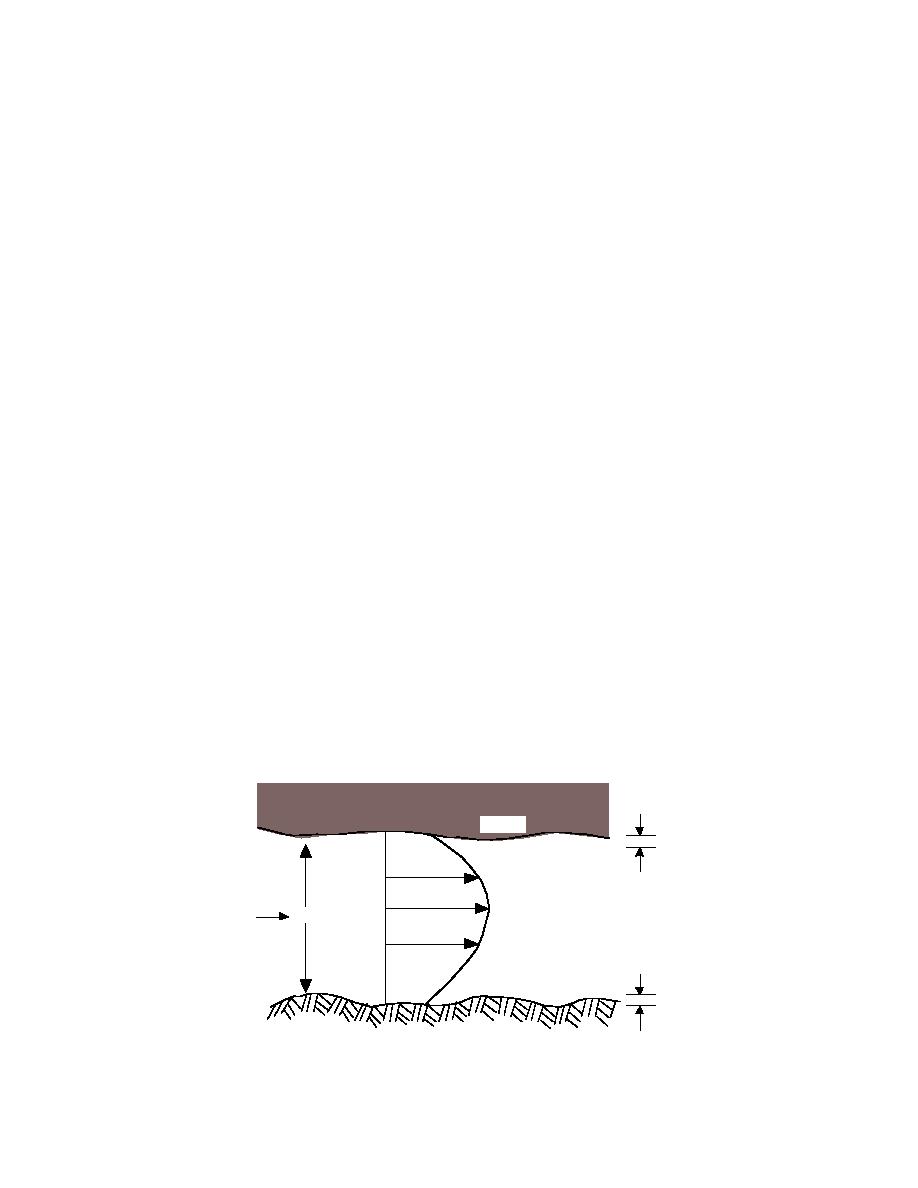
Ice cover roughness (ni)

Ice cover roughness is the most thoroughly ex-

is, dividing the flow area into separate layers af-

plored hydraulic property of ice covers. In fact,

fected by the bed and the ice cover (Fig. 5). A com-

the biennial River Ice Workshops sponsored by the

posite channel roughness coefficient is calculated

Canadian government (see, e.g., Ismail 1997), be-

through application of standard flow equations

gan as a workshop on the hydraulic resistance of

such as Manning's equation or the Darcy-

river ice in 1980 largely devoted to developing an

Weisbach equation (numerous researchers) or

understanding of ice cover roughness (Tsang and

boundary-layer theory (e.g., Gogus and Tatinclaux

Beltaos 1980). Yet there is still a need to obtain re-

1981). Given an estimate of bed roughness, the

liable field measurements of ice jams roughness.

roughness of the underside of the ice can then be

calculated using a formula such as the Belokon-

A review of formulas for computing composite

roughness coefficients as well as a discussion of

Sabaneev formula (eq 11). Roughness has also been

roughness estimates made by others (Lotter 1932,

calculated from estimates of the shear stress on

1941; Belokon 1938, 1940; Panov 1960) is included

the underside of the ice cover (e.g., Knowles and

in Nezhikhovskiy (1964). He suggests that many

Hodgins 1980, Hara et al. 1997). Unfortunately, few

published values of ni and nc are incorrect due to

data useful in calculating roughness exist, particu-

errors in measured and estimated discharge and

larly for breakup jams. Also, the presence of an

water slope. Also, the smoothing of the bottom

ice jam can cause changes in bed roughness, which

Ice

ni,, cii, fi

ni c

kii

viV

τiτi =ττb =oo

= b=

vma

Vmaxx

nb , cb,, ffbb

Bed

Figure 5. Variables important in flow beneath an ice cover.

Index

Privacy Statement
Press Release
Contact