been known to progress by juxtaposition at veloci-
analyses had been static in that they neglected the
ties more than three times greater than the critical
angular momentum of the rotating blocks). They
velocity they predicted. Using a different ap-
found that the Froude criteria of Pariset and
proach, Tremblay and Thibeault (1980) proposed
Hausser (1961) and Ashton (1974) underpredicted
a critical velocity criterion for the Milles Iles River
the critical Froude number for stability, particu-
(Quebec) based on the Chezy formula that in-
larly for small ratios of floe thickness to depth.
cluded floe size and ice discharge.
They did find good agreement, however, with the
Later researchers (e.g., Uzuner and Kennedy
shallow water criterion for stability presented by
1972, 1974; Ashton 1974; Uzuner 1975; Michel 1978;
Daly (1984):
Tatinclaux and Gogus 1981) used both laboratory
experiments and analysis to arrive at a rational
4 1 - ts β
3
Froude number to describe the limits of the rota-
H
v
F=
≤
tional stability of the ice floes. Generally, a densi-
3
gtb
2
2
tb tb ρi
ts
(2)
metric Froude number was used, with a length
1 - 1 - -
H L ρ
H
scale based on some ratio between the ice block
thickness and water depth, modified by the dif-
ference in the densities of water, ρ, and ice, ρi.
where tb is ice block thickness, L is ice block length,
Ashton (1974) successfully described the experi-
H is upstream water depth, and β is a coefficient
mental data using an analysis based on the "no-
that is independent of underturning velocity, and
spill" condition, which postulates that the limit of
block length, thickness, and density, determined
rotational stability occurs when the upper, up-
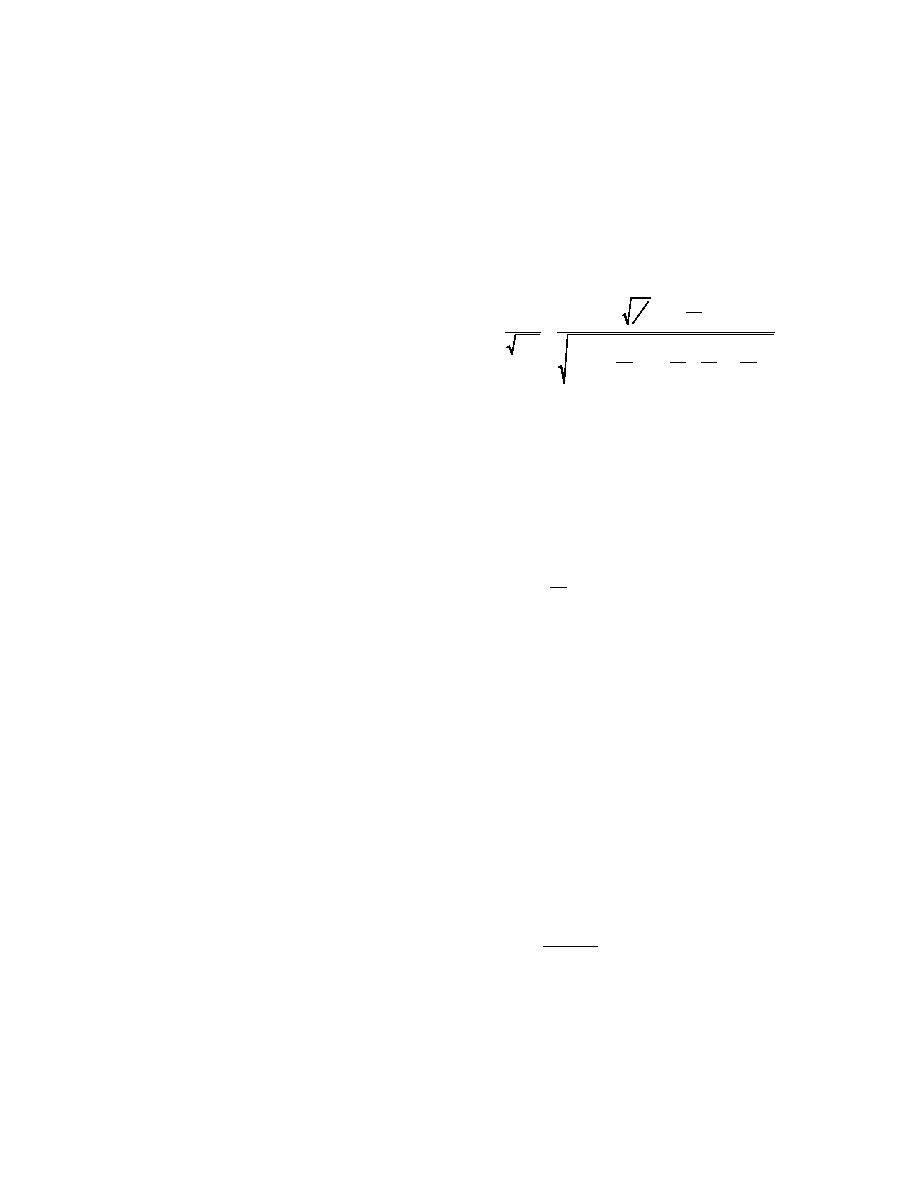
to be equal to 0.262. A definition sketch is given in
stream corner of the block becomes submerged.
Figure 2. The submerged depth of the ice block, ts,
He assumed that the underturning moment was
is calculated using
caused by the acceleration of flow under the block
because of the constriction caused by the block.
Despite the obvious problem that the constriction
ρ
ts = i tb .
of flow would be negligible in deep water,
(3)
ρ
Ashton's criterion was widely adopted.
Daly and Axelson (1990) demonstrated that
floating blocks have a well-defined maximum
Daly (1984) noted that this equation, developed
righting moment. They noted that the limit of ro-
as a simple curve fit to data from Uzuner and
tational stability has been reached when the
Kennedy (1972), Ashton (1974), and Larsen (1975),
underturning moments exceed this maximum and
is not strictly applicable to deep water (ice block
a no-spill condition was not necessary. They de-
thickness-to-depth ratios less than about 0.1).
veloped an analytical expression for the limit of
More recently, Andres (1999) has proposed the
rotational stability in terms of the hydrostatic right-
use of a dimensionless stability number to deter-
ing moment of the block, expressed in the form of
mine whether juxtaposition or shoving will domi-
a densimetric Froude number. Their work was
nate the ice cover formation process under differ-
incorporated by McGilvary and Coutermarsh
ent hydrologic and meteorological conditions. His
(1992) in a dynamic analysis of ice block stability
analysis includes the effects of temperature in the
based on careful measurements of the pressure
form of air temperature (Ta), the thermal conduc-
distributions around the leading edge and under-
tivity of the ice (ki), and the latent heat of fusion of
side of a model ice floe for various flow depths
the water (Lf). The dimensionless stability num-
(Coutermarsh and McGilvary 1991, 1993). This
ber takes the form
pressure distribution, produced by the accelera-
tion of the flow as it passed under the block, cre-
TaBki
X=
ates an underturning moment acting on the block
(4)
QSfρiLf
that could cause underturning in both deep and
shallow water.
McGilvary and Coutermarsh (1992) further ex-
where Q is discharge, B is river width, and Sf is
tended the analysis by including the angular mo-
the water slope. A typical value of the latent heat
mentum of the block, and demonstrated that the
of fusion of water is 334 J/g (Batchelor 1967). The
angular momentum could be an important factor
thermal conductivity of the ice is related to tem-
in causing blocks to underturn (all of the previous
perature by the following equation (USACE 1999):
3



 Previous Page
Previous Page
