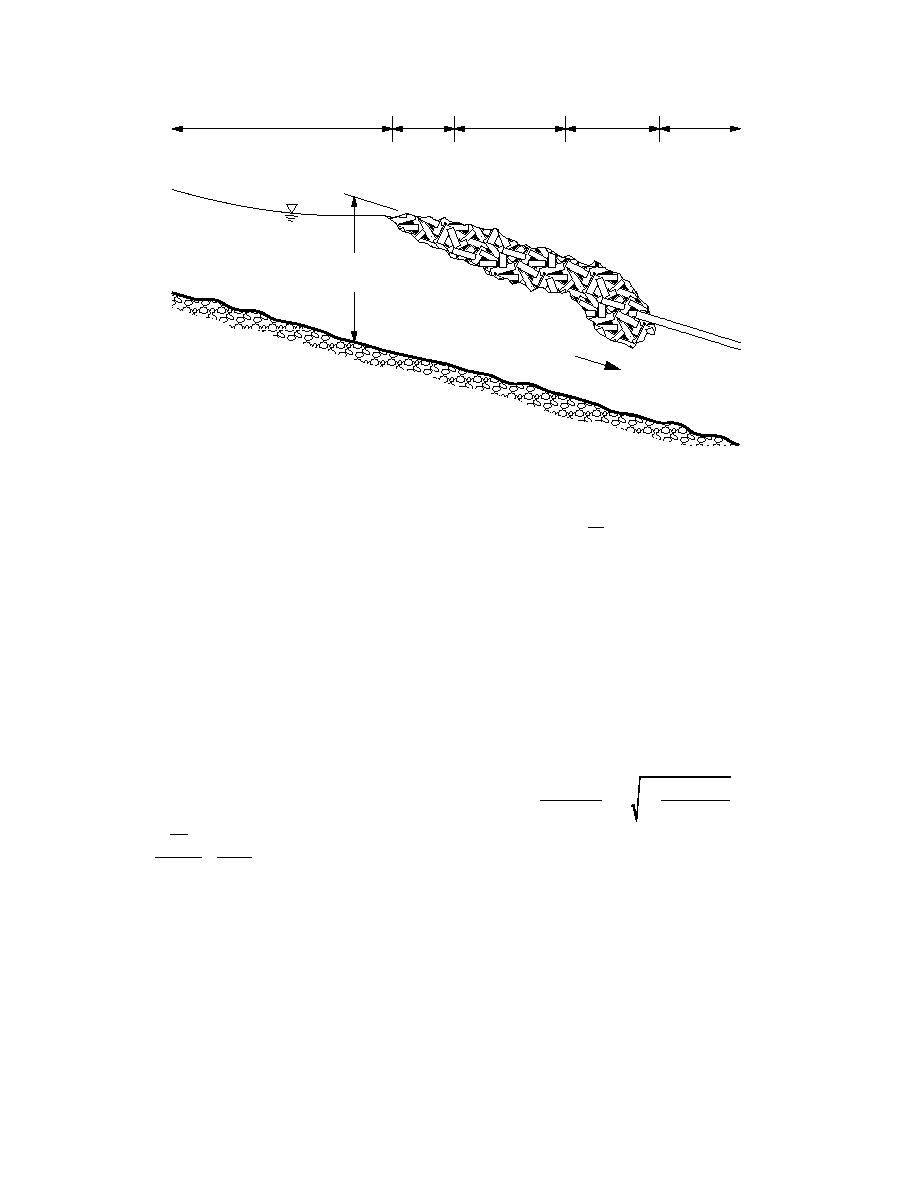
Transition
Transition
Uniform
Transition
Uniform
"Equilibrium"
Section
Ice Accumulation
Maximum Depth Given
by Equilibrium Section
Solid Ice
Cover
Flow
Figure 4. Typical breakup ice jam with equilibrium section.
ρ
0 = gρi 1 - i η2 - ( gρiSf - 2Ci )η - τB (17)
determine when the assumption of steady state
ρ
will be violated to a sufficient degree that unsteady
where is the coefficient of internal strength of
methods should be utilized. Preliminary results
the ice cover, sometimes called the friction coeffi-
indicate that the steady-state assumption is accept-
cient, and Ci is the cohesion. Cohesion is often
able in many cases.
neglected for breakup ice jams, but can be impor-
A number of expressions are available for cal-
tant for freezeup jams. The shear stress on the
culating the equilibrium ice jam thickness in
underside of the jam, τ, can be expressed as
breakup ice jams, that is, the uniform thickness
section of an ice jam that has formed through
τ = ρgRiSf .
(18)
shoving of the ice (Pariset et al. 1966; Uzuner and
Kennedy 1974; Beltaos 1978, 1995). The expression
For negligible cohesion (Ci = 0), eq 17 yields the
selected for use in HEC-RAS is based on
following expression for the equilibrium ice jam
the ice-jam force balance equation in which the
thickness:
stresses within the jam are balanced against the
external stresses on the jam (USACE 1997, Daly
4(1-si )Ri
BSf
1 + 1 +
η=
et al. 1998):
2(1 - si )
(19)
siBSf
( ) + 2τ b η = ρ gS η + τ
d σxη
where si is specific gravity of ice (ρi/ρ). The water
(16)
i
f
dx
B
surface elevation in the equilibrium section of a
breakup ice jam, h, is calculated by
where σx is the stress in the streamwise direction
h = yi + si η.
x (assumed to be constant across the width of the
(20)
channel, B), η is the thickness of the ice accumula-
In summary, application of equilibrium ice
banks, and τ is the shear stress on the underside
thickness models (e.g., eq 19) will require some
of the jam. This force balance, expressed by Ashton
knowledge or estimation of the following ice prop-
erties: Ci, , ρ, ρi, nb, ni, nc, L, and H, of which two,
(1986) in the form below, was used by Tuthill et al.
ρ and ρi, are well known.
(1998) in the ICETHK option of HEC-2:
7





 Previous Page
Previous Page
