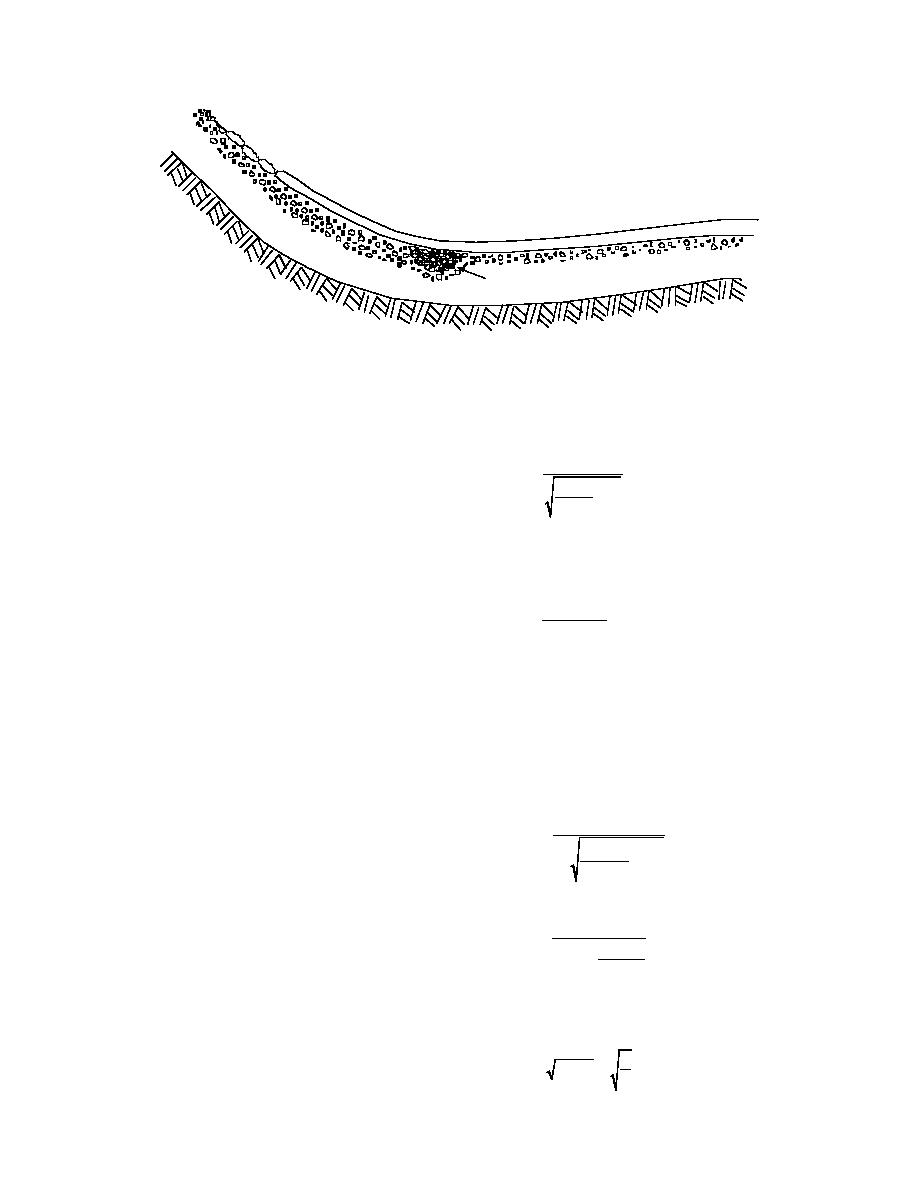
Ice Cover
Frazil
Deposit
Figure 3. Frazil deposit formation.
decreased from 0.9 m/s in early winter to 0.6 m/s
The dimensionless ice transport capacity is de-
in late winter on the LaGrande River, Quebec. Daly
scribed by
(1994) attributes reported variations in critical ve-
locity to factors such as the form of the frazil, the
qi
Φ=
length of travel, and the degree of supercooling in
ρ - ρi 3
the river. Michel (1984) suggests that variations in
(7)
gd
ρ
critical velocity may be explained by the physical
state of the frazil particles. In his experience, criti-
cal velocities decrease with age from a high of
in which qi is the ice transport capacity per unit
about 1.4 m/s for active, or recently formed, frazil
width and d is the particle diameter. The dimen-
to a low of about 0.6 m/s for aged frazil floes.
sionless flow strength is calculated using
These variations, along with variations in the
τ
Θ=
critical velocity between rivers and between dif-
(ρ - ρi )gd
(8)
ferent reaches on the same river, made it difficult
to apply this method. In view of these difficulties,
where τ is the shear force on the underside of
Sun and Shen (1988) proposed an empirical
the ice cover. Laboratory studies reported by Shen
method to estimate ice thickness based on Froude
and Wang (1995) suggested that the dimension-
number, similar to the approach taken for juxta-
less parameters Φ and Θ in eq 6 and 7 should
position. The stability criteria resulting from labo-
be modified to account for the effect of the shape
ratory studies and analytical analyses (e.g., Ashton
of the particles, resulting in the following formu-
1974, Gogus and Tatinclaux 1981, Daly and
lations:
Axelson 1990) have taken the form of some varia-
tion on the densimetric Froude number. However,
Starosolzky (1981) suggested that scatter in experi-
qi
Φn =
mental data for parallelepipeds using this method
(ρ - ρi ) gd
could be explained by a bed-load transport ap-
3
(9)
Cf
n
ρ
proach.
Although not yet applied to blocks, bed load
and
transport has been applied to frazil ice by Shen
2
and Wang (1992), who proposed a new method to
u*
Θn =
(ρ - ρi)
analyze frazil transport based on the concept that
2
(10)
Cf gdn
the movement of the ice particles is caused by the
ρ
shear stress acting on the particles. Essentially, the
where Cf is a fall velocity coefficient, dn is the nomi-
method relies on the functional relationship be-
tween the dimensionless ice transport capacity, Φ,
nal particle diameter, and u* is the shear velocity:
and the dimensionless flow strength, Θ:
τ
u* = gRiSf =
Φ = f (Θ).
(11)
(6)
ρ
5



 Previous Page
Previous Page
