Solution procedure-continue - CR99_070028

Solution procedure

Solution procedure-continue - CR99_070029

CR99_07
Page Navigation
18

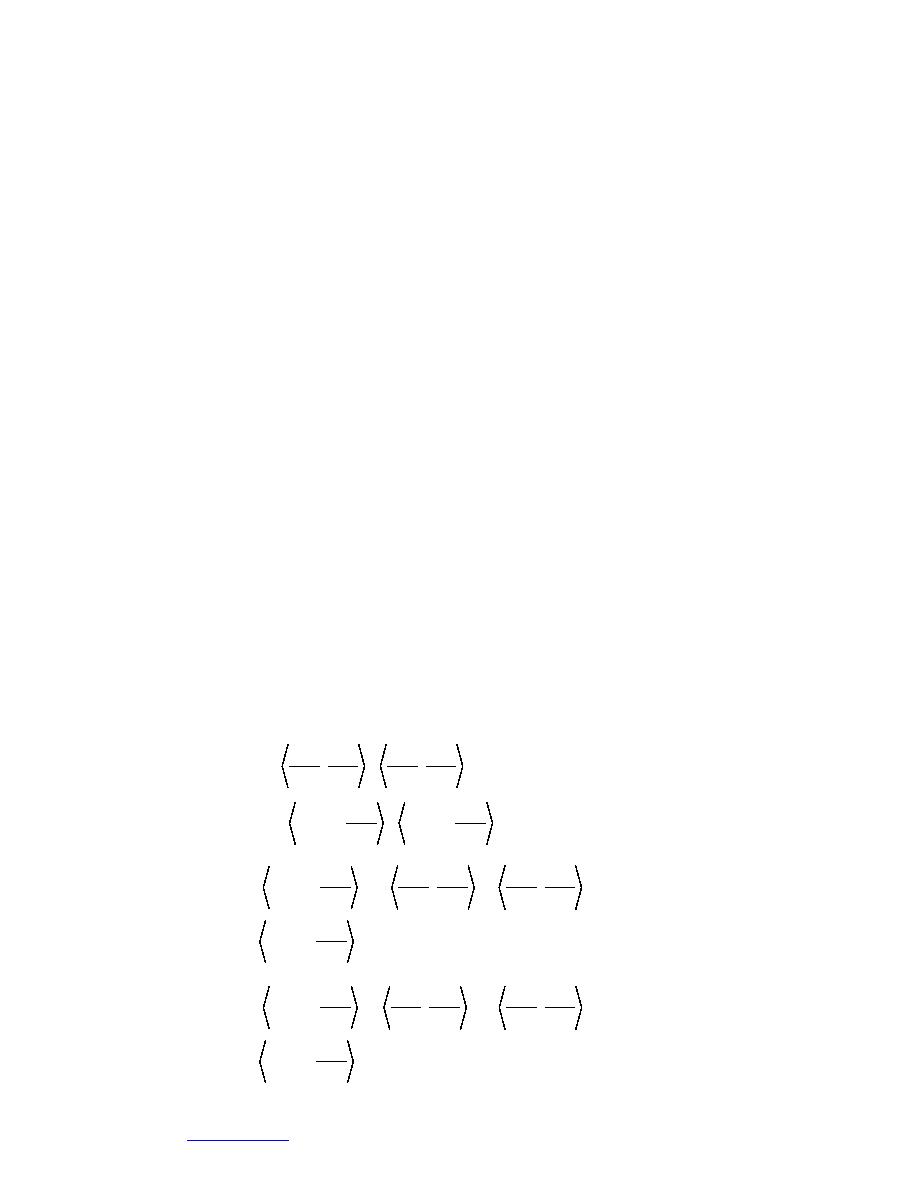
tion and the Newton-Raphson method can utilize a relaxation procedure, which

consists of determining the weighted average of the old and new solutions. The

new solution = θ(old solution) + (1 θ) new solution

where the weighting or relaxation factor (θ) varies between 0.005 and 0.25 depend-

ing on the maximum amount of change from the previous solution and the solu-

tion method. This range was determined by trial and error in an effort to improve

the convergence rate. No formal optimization approach was attempted, and these

values are not necessarily the best values. High values caused oscillations in the

direct substitution solutions to high Rayleigh number problems (greater than 105)

for the vertical enclosure problem, and once large oscillations begin, the procedure

will not converge to a solution.

The procedure was considered to have converged to the steady-state solution

when the largest change in each variable between successive solutions was less

than 0.01%. Changes this small or smaller were found to produce no significant

difference in the heat flux calculations through the enclosure sides.

The global matrix is 3n+p by 3n+p for the fluid elements plus n by n for the ele-

ments that are a solid material, where n is the number of nodes and p is the num-

ber of nodes associated with the pressure formulation (four per element). This cal-

culation of matrix size is reduced by the number of solid-fluid boundary nodes

(which were counted twice in the above analysis). There are 28 degrees of free-

dom for each element specified as a fluid and 8 degrees of freedom for those speci-

fied as a solid.

The global matrix for the direct substitution method has the form

0  T  R2

A8 A4 u  0 

  = 

A7 A5 v  R1 

    

A5T 0  p  0 

+ Cv  u m , N j ,

 + h∫s Ni N j ds

A3 = uim , N j ,

A7 = u m , N j ,

Western Governors University

Privacy Statement
Press Release
Contact

Integrated Publishing, Inc. - A (SDVOSB) Service Disabled Veteran Owned Small Business