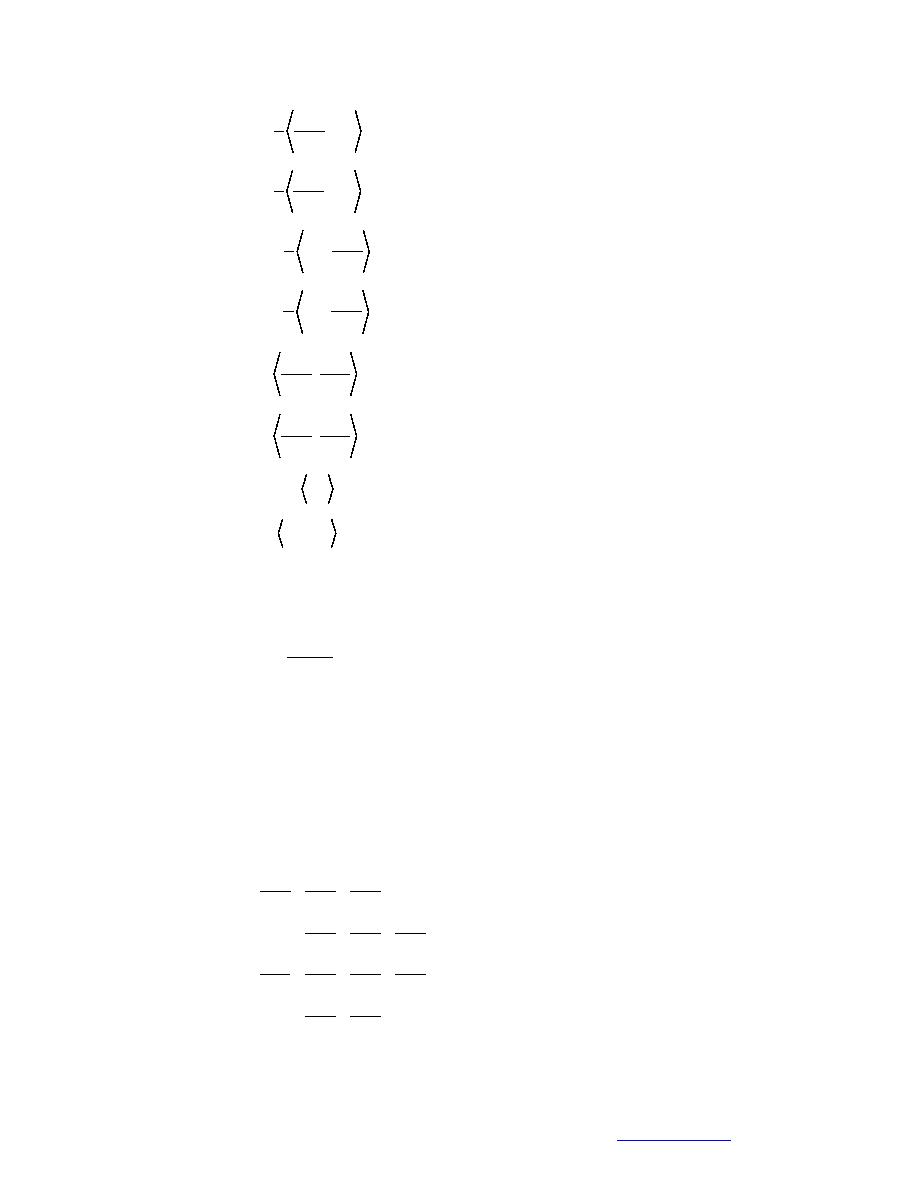
Ni
1
p
A4 = -
(101)
, Nj
ρ
x
Ni
1
p
A5 = -
(102)
, Nj
ρ
y
p Ni
1
A4T = -
(103)
Nj ,
ρ
x
p Ni
1
A5T = -
(104)
Nj ,
ρ
y
Nj
Ni
A8 = υ
(105)
,
y
x
Nj
Ni
A9 = υ
(106)
,
x
y
R1 = gβTref Ni
(107)
A1 = gβ Ni , N j
(108)
R2 = ∫ hN jT∞ ds - ∫ φN jds .
(109)
s
s
The Newton-Raphson method, in its general one-dimensional form, is
f (ω 0 )
ω = ω0 -
(110)
f ' (ω 0 )
where ω is the root of the function f (Hornbeck 1975). In multidimensional form,
following Gartling (1987),
new solution = old solution J1 (old solution)R(old solution)
(111)
where J1 is the inverse of the Jacobian matrix of eq 6871 and R is the vector of the
residuals obtained by substituting the old solution into eq 6871. The Jacobian
matrix is
RT
RT
RT
0
T
u
v
Ru
Ru
Ru
0
p
u
v
J=
Rv
Rv
Rv
Rv
(112)
p
T
u
v
Rp
Rp
0
0
u
v
where RT , Ru, Rv, and Rp are eq 6871, respectively.
19
Back to Contents
Previous Page
