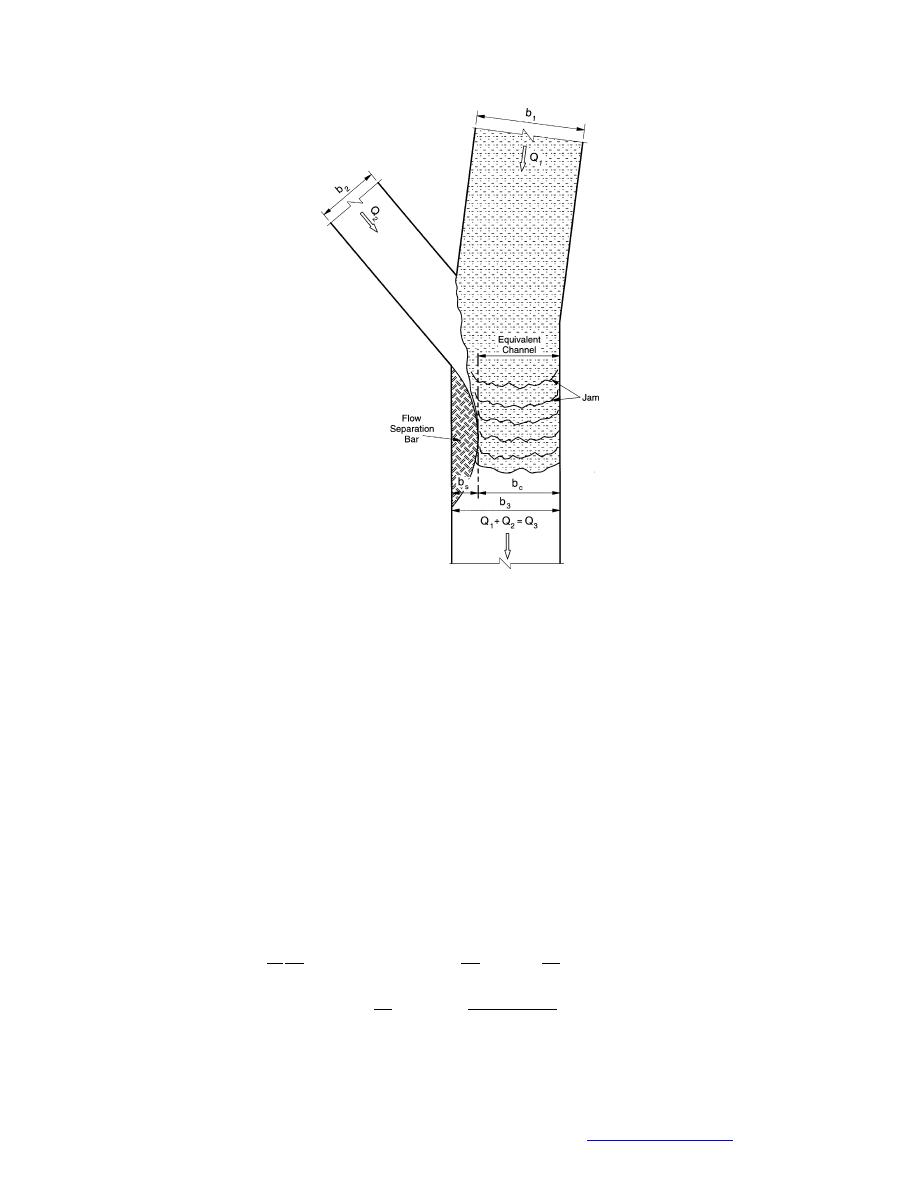
Figure 32. Ice jam formation at confluence nar-
rowed by a bar.
force F″merge1 can be approximated as the lateral pressure exerted by ice moving
from channel 2, σz2, multiplied by the contact area parallel to the direction of flow
in channel 1, η2(b2/sin α + be). The length be can only be estimated, because no
predictive relationship presently exists for it. As an approximation, be ≈ bs, though
be always exceeds bs.
Ice will not jam if ΣF Fmerge > 0, because the net force driving ice in channel 2 is
sufficient to overcome the additional resistance generated by the lateral pressure
of ice moving from channel 1.
Equation 21 can be used in quasi-steady formulation of ice movement and jam-
ming in confluences. A difficulty in the formulation is estimation of the width b3
bc; or rather bc. For a one-dimensional formulation, an approximation would be to
set b3 bc ≈ b3. This approximation is somewhat crude, but reasonable given all the
other uncertainties associated with estimation of jam behavior. Inclusion of F′merge1
and F″merge1 would modify the force formulation, such as proposed by Uzuner
and Kennedy (1976), for a static floating ice jam:
ρ η
(
)
(η1σ x1 ) - y η1τxy1
+ si1ρgη1 sin(θ + ϕ)1 -
τi1 cos i
ρ x1
x
b + b2 / sin α
(22)
bd
- σ z2 η2 (
) - 1σ z2 η2 ( s
)=0
b1
b1
where σx, τxy, τi, are the normal stress in the streamwise direction, the shear stress
at the banks, and the shear on the underside of the cover, respectively. The angle θ
39
Back to contents page




 Previous Page
Previous Page
