Chemical equilibrium modeling considerations
To model the chemistry of any aqueous electrolyte solution, the chemical potential of
each modeled constituent must be estimated either explicitly or implicitly. The most effi-
cient means of estimating the single-ion chemical potential of a solute is by
m γ
B(aq) = Θ(aq) + RT ln BΘB .
(35)
B
mB
Θ
Both the standard-state chemical potential of the solute [ B(aq)] and the single-ion activity
coefficient γB are affected by temperature. These effects are presented in Figures 8 and 9.
Further, ice is nearly a pure phase. As aqueous solutions are cooled below their freezing
points, ice forms, excluding solutes to the remaining liquid-water solutions. Accordingly,
the aqueous solutions at subzero temperatures are typically brines, the activity coefficients
for which must be estimated by elaborate models such as that of Pitzer and his coworkers.
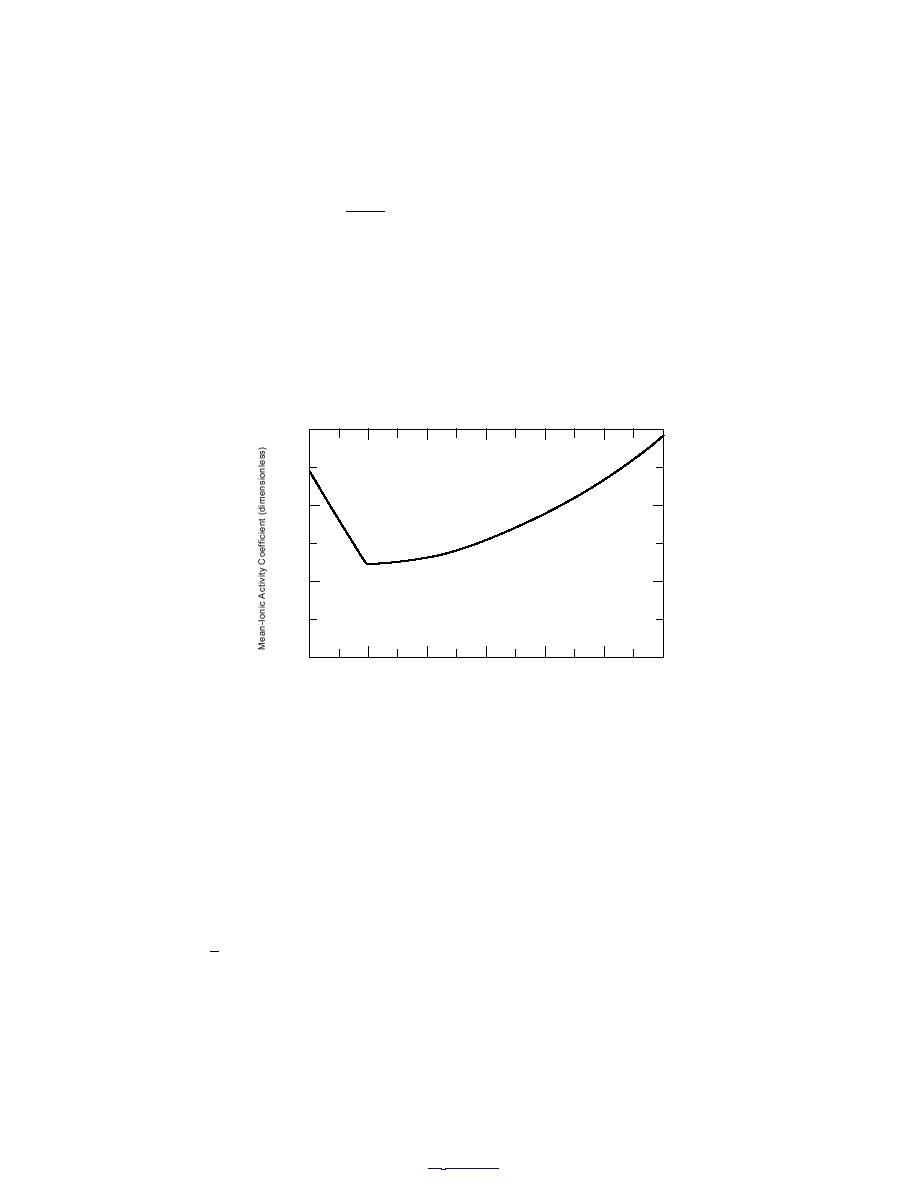
(For a further discussion, see Pitzer 1991 and Spencer et al. 1990.) Figure 10 shows the iso-
thermal, isobaric changes in the activity coefficient of a salt (NaCl) with its concentration.
Colligative properties: freezing point depression
1.0
0.8
0.6
0.4
0
1
2
3
4
5
6
NaCI Molality (mol kg1)
Figure 10. Mean-ionic activity coefficient of NaCl(aq) (p = 0.1
MPa, T = 298.15 K) as function of molality.
While liquid water is an almost universal solvent, ice is generally a very pure phase. The
freezing point of an aqueous solution is depressed proportionately to the concentrations of
its solutes. The thermodynamics of this behavior is fairly straightforward. The discussion
here follows closely that of Atkins (1990).
At equilibrium, the chemical potentials of the solvent in the liquid and solids phases are
equal:
A(s) = A(l) .
(36)
Since the standard state for the solvent is pure solvent substance:
O (l) d=f * (l)
e
(37)
A
A
by eq 29 the following relation can be derived:
* (s) = * (l) + RT s+ l ln aA
(38)
A
A
is obtained, Ts+l representing the freezing temperature. If it is assumed that aA ≡ xA (i.e.,
fA ≡ 1),
15
TO CONTENTS




 Previous Page
Previous Page
