If the solution is dilute, then lnx = ln(1 x2) = x2, where
P
374, 220 atm
x2 is the mole fraction of the solute, and because n2<<n,
n
- x2 ≈ - 2
(44)
n
where n refers to the number of moles. Thus, substitut-
ing eq 44 into eq 43 yields
1 atm
n2 RT
Π=
(45)
o
nV
o
but V ≈ nV , so
Π = cRT
(46)
~
611 Pa
where c is the solute concentration (mol m3). The con-
~
cept of osmotic pressure is useful in formulating expres-
sions for total soil water pressure because soil water
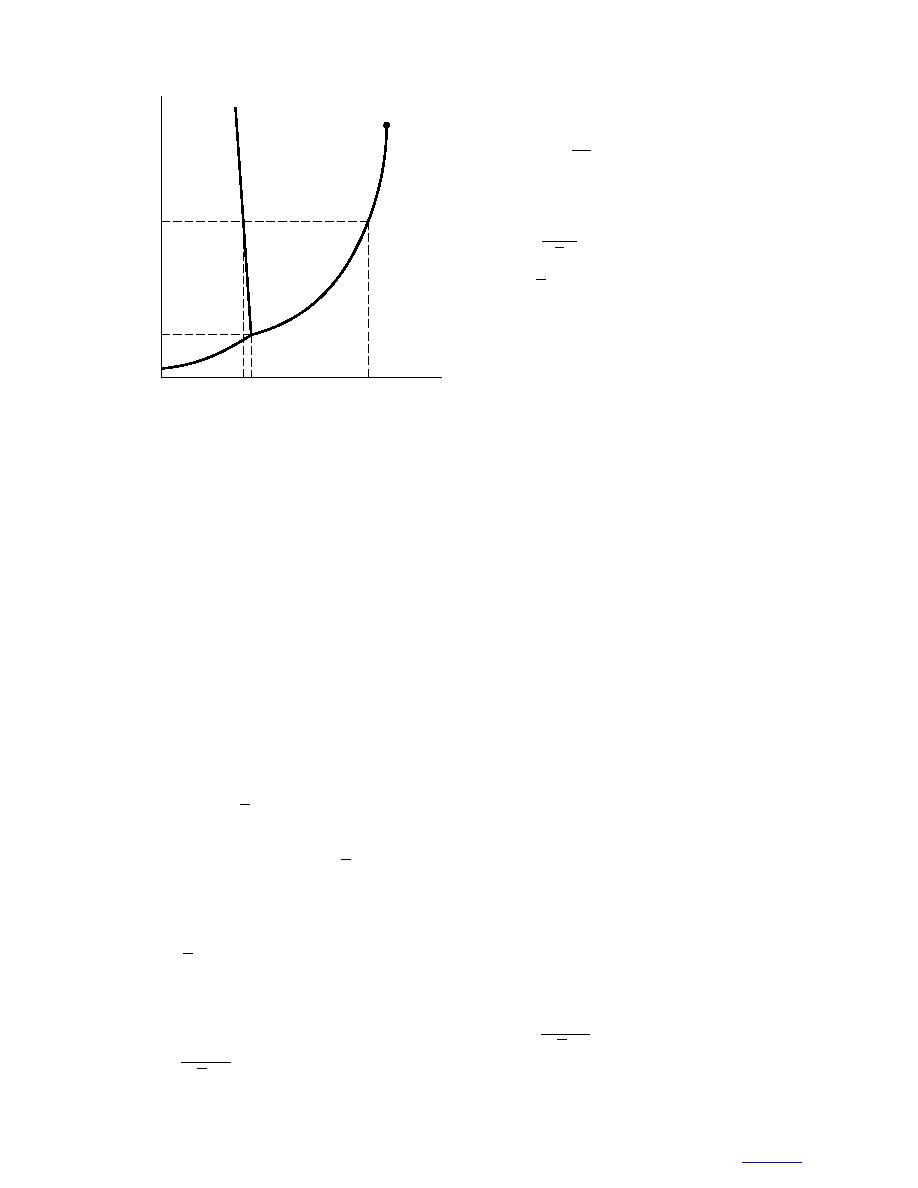
0 0.01
100
contains solutes. Furthermore, the influence of soil par-
T ( C)
ticle surfaces on the chemical potential of the soil water
Figure 2. Phase diagram for water.
can be "approximated" as solutes.
the pressure and temperature conditions for phases in
Summary
equilibrium.
Fundamental thermodynamic principles have been
reviewed in the above sections. The relations and con-
Osmotic pressure
cepts that are particularly useful in studying the physi-
Osmotic pressure, Π, is the pressure required to
cal processes associated with freezing soil are
maintain equilibrium between a solution and the pure
1. Thermodynamic equilibrium requires a balance
solvent across a semi-permeable membrane through
of thermal, mechanical, and chemical forces. Thermal
which the solvent, but not the solute, can diffuse. The
equilibrium is reached when temperatures are equal,
osmotic pressure is easily determined using the chem-
mechanical equilibrium is reached when there is a bal-
ical potential requirement of equilibrium. For the sol-
ance of mechanical forces, and chemical equilibrium
vent on both sides of the membrane,
is reached when the chemical potentials of all compo-
nents of the system are equal.
(T, P + Π, x) = o (T, P).
(39)
2. The general equation for mechanical equilibrium
between two phases--i.e., the interface is curved, rather
From eq 25 we know that (T, P + Π, x) = o(T, P + Π)
than planar--is (Pa Pb)dV = ΨdAr (eq 17).
+ RTlnx. Substituting this into eq 39 results in
This equation applies to interfaces between all phases
of a substance (solid/liquid, vapor/liquid, and solid/
o (T, P + Π) + RTlnx = o (T, P).
(40)
vapor interfaces) and is the physical reason for capil-
lary rise of liquids in porous materials.
o
Using eq 34, d o = V dP and integrating from P to
3. The GibbsDuhem equation,
P + Π, we get
∑ ηi d i = -SdT + VdP
P+Π
o
∫
o (T, P + Π) - o (T, P) =
(41)
V dP .
i
P
(eq 31), is useful when applied to water in freezing soils.
4. The concept of osmotic pressure is useful in for-
Substituting eq 41 into 40 yields
mulating expressions for total soil water pressure. This
P+Π
is because soil water contains solutes; in addition, the
∫
o
V dP + RT lnx = 0 .
(42)
influence of soil particle surfaces can be "approximated"
as solutes. Expressions for the osmotic potential of a
P
dilute solution are
For an incompressible solvent in an ideal solution the
- RT lnx
molar volume remains constant, and
Π=
o
- RT lnx
V
Π=
(43)
.
(eq 45) and Π = cRT (eq 46).
~
o
V
7




 Previous Page
Previous Page
