900
by cutting a cylinder out of the ice using a bandsaw
and further cutting it into sample disks as described
760
above. These were stored in the coldroom at about
10C for a day before testing.
Ice
820
We used the CRREL snow load frame for the
Snow
flexural strength tests. This was equipped with an
780
Interface, Inc., 250-pound load cell and Schaevitz
MagneRule displacement transducer. The cylindrical
0 seconds
740
30 seconds
indenter, attached to the load cell, was 1 cm in diameter
60 seconds
with a flat tip. It was centered over a short section of
700
iron pipe with an outside diameter of 6 in. (15 cm) and
3.5
5.5
6.5
7.0
4.0
4.5
5.0
6.0
Compaction Pressure (MPa)
a 0.5-in. (1.25-cm) wall thickness, so that the brick
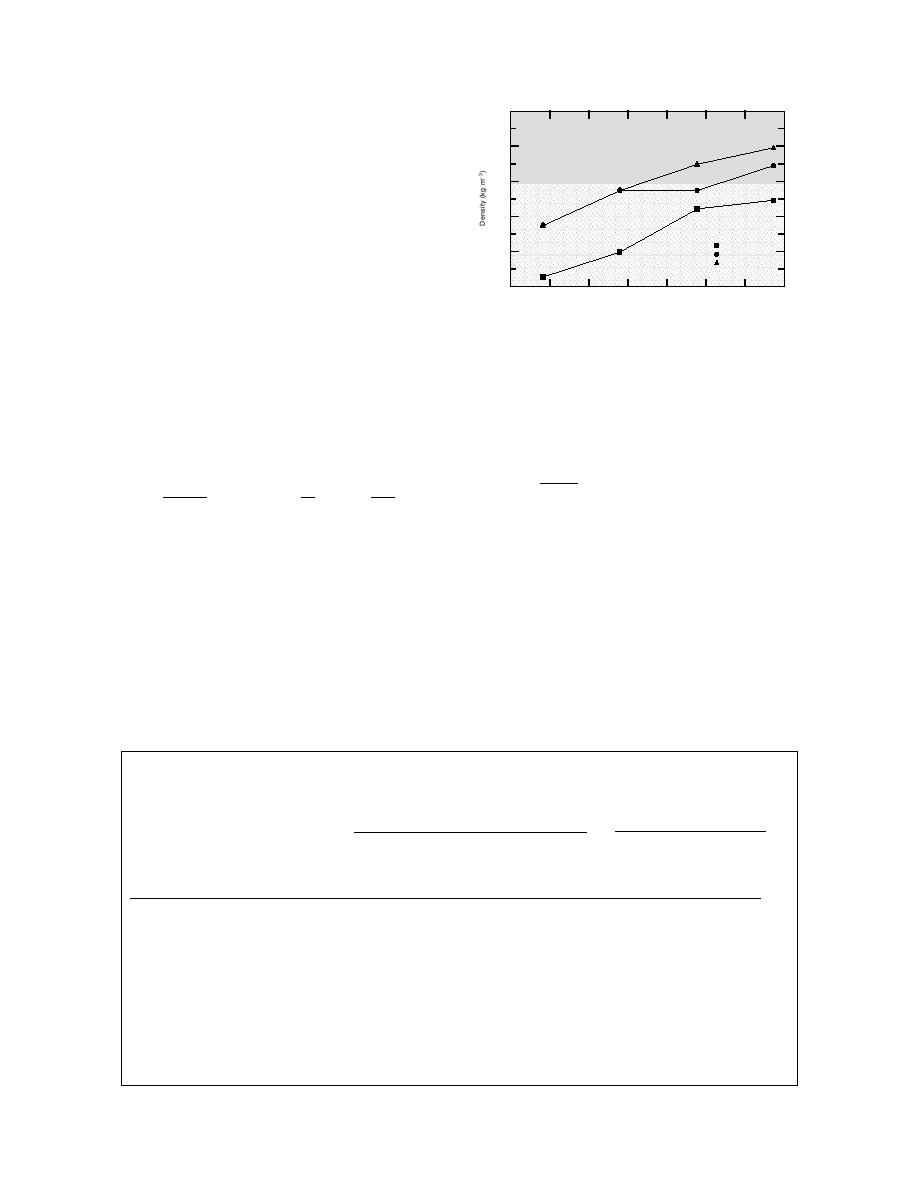
Figure 9. Density in kg/m3 of snow compacted at
samples fit across the opening without overhang. The
different pressures. The different data series rep-
press speed, without load, was 0.06 cm/sec. The
resent samples that were held at the final pressure
apparatus is shown in Figure 8.
for 0, 30, and 60 seconds.
The flexural strength of the plates was calculated
Our supporting ring had an inside diameter of 12.65
using the method described by Yakovlev (1971) and
cm, giving r = 6.33, and our indenter was a 1-cm cylin-
Lavrov (1969). The equation yields the maximum
der, giving r0= 0.5. Substituting these values, eq 3
normal stress in a freely supported plate of constant
becomes
thickness with a centrally located circular load:
2.09P
.
(4)
σf = -
r02
(
)
(
)
3P
r
σf = -
m + m + 1 ln - m - 1
(3)
h2
2πmh2
4r 2
r0
Results
Table 3 gives the average flexural strength for each
σf = flexural strength (kg/cm2), later
of the sample series. The strength was calculated using
where
converted to MPa
eq 4, and this value was then multipied by 0.65, the
P = maximum load (kg)
empirical coefficient determined by Lavrov to
m = inverse of Poisson's ratio
normalize the round plate tests with respect to beam
h = plate thickness (cm)
bending tests. The strength values have been converted
to MPa.
r = the inside radius of the supporting ring
Table 4 gives the flexural strength determined for
(cm)
various types of ice using beam bending and round plate
r0 = the radius (cm) of the load (indenter).
methods. The round plate data have been normalized
as above. The strengths calculated for the three series
Assuming a Poisson's ratio of 0.33, m becomes 3.
Table 4. Comparison of the flexural strength of ice under different conditions. Test conditions and ice
type are given, where known.
Beams
Disks
Test
Measured
Test
Measured
Adjusted
temperature
flexural
temperature
flexural
flexural
(C)
(C)
strength
strength
strength
Type of ice
(MPa)
(MPa)
(MPa)
Sea ice (3 ‰) (Lavrov 1969)
1
0.75537
1
1.10853
0.721035
Sea ice (0.5 ‰) (Lavrov 1969)
2.5
0.981
2.5
1.55979
1.014354
Artificial ice (Lavrov 1969)
5
1.372.74
4
2.3544
1.4715
Lake ice (S2) (Lavrov 1969)
0.5
0.882.26
Lake ice (S2) (this study)
10
2.0601
1.3734
Lake ice (Gow 1977)
0
0.231.52
Freshwater (Schwarz and Weeks 1977)
1.03
Snow ice (T1) (Stearns 1964)
15
2.3544
Snow ice (T1) (this study)
10
3.1392
2.0601
Unknown (Gold 1977)
3.534.51
2.262.94
CFG ice (this study)
10
4.024.91
2.553.14
8




 Previous Page
Previous Page
