scattering in snow (Bohren and Barkstrom 1974,
functions are extremely difficult to measure. There
Wiscombe and Warren 1980). A thorough general
is, however, one simplifying aspect to scattering
discussion of scattering can be found in van de
in sea ice in the optical regime: it can be assumed
Hulst (1981) and Bohren and Huffman (1983).
to be independent of wavelength. The wavelength
Observations of scattering parameters are lim-
dependence of the real portion of the index of
ited. Perovich and Grenfell (1982) estimated scat-
refraction for ice, brine and air is very weak at
tering coefficients for young ice from observa-
optical wavelengths and typically is assumed to
tions of albedo and transmittance. They found
be constant with wavelength (Grenfell 1983, 1991).
that scattering coefficients ranged from 8.9 m1
Optical wavelengths are on the order of tenths of
for melting young ice to 19.6 m1 for cold young
a micrometer to micrometers. The inclusions in
ice to 420 m1 for very cold young ice with pre-
sea ice have sizes on the order of tenths of a
millimeter for brine pockets to millimeters for air
cipitated solid salts present. Grenfell and Hedrick
bubbles. Since the scatterers are much bigger than
(1983) used small samples of young ice to mea-
the wavelength and the scatterers are far apart,
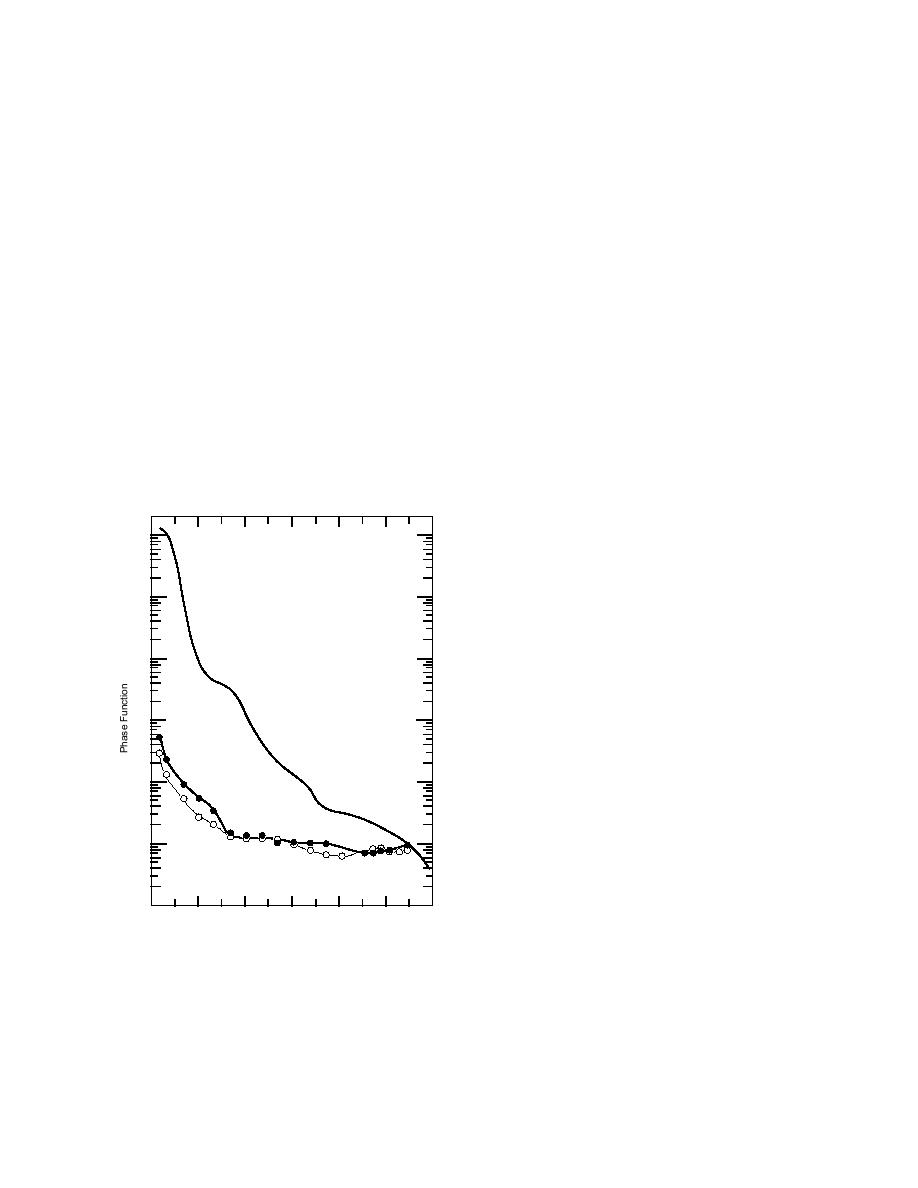
sure phase functions for sea ice. Phase functions
for columnar ice samples grown at 10C and
contributions due to diffraction and interference
30C are shown in Figure 7. The phase function
can be ignored (Grenfell 1983, Bohren and Huff-
man 1983). The result of the weak wavelength
is strongly forward-peaked, with forward scat-
dependence of n, and the fact that the size of the
tering being more than a factor of 50 greater than
scatterers is much larger than the wavelength, is
side or backward scattering. However, although
that scattering coefficients and phase functions
small samples were used, there was still multiple
for sea ice can be assumed to be constant with
scattering, and consequently the results represent
wavelength (Grenfell 1983, 1991, Perovich 1993).
only an approximation to the true single scatter-
A similar argument is made when analyzing
ing albedo and phase function. Multiple scatter-
ing tends to smooth and reduce the angular de-
pendence of the measured phase function.
Numerical calculations have been used to
10 5
supplement the relatively sparse observational
data (Grenfell 1983, 1991). Phase functions are
calculated using a Mie scattering model with the
10 4
indices of refraction for ice and brine and inclu-
sion size distributions as input parameters (Bohren
and Huffman 1983). A calculated phase function
for sea ice at 30C with brine pockets with a
10 3
radius of 0.02 mm (Light 1995) is compared to
observed values in Figure 7. As expected, the cal-
culated phase function is more strongly forward-
10 2
peaked than the multiply-scattered observed.
c
Though we do not have a quantitative under-
standing of the relationship between scattering
1
and ice physical properties, a qualitative grasp is
10
a
sufficient for our purposes. To interpret observa-
b
tions of optical properties the important theoreti-
cal points are 1) absorption coefficients for ice
0
10
and brine depend strongly on wavelength, 2) scat-
tering coefficients and phase functions for sea ice
are constant with wavelength, 3) increasing the
1
10
number of inclusions in sea ice increases the
0
30
60
90
120
150
180
Angle
amount of scattering, 4) air bubbles scatter more
Figure 7. Observed (Grenfell and Hedrick 1983) and
strongly than brine pockets, and 5) scattering in
calculated (from Light 1995) phase functions for sea
sea ice is strongly forward peaked. With this
ice. 0 is forward scattering and 180 is backward scat-
theoretical foundation regarding the underly-
tering: a) observations of ice grown at 30C, b) obser-
ing physics of radiative transfer in sea ice, it is
vations of ice grown at 10C, and c) calculated esti-
time to revisit the question of "What is the albedo
mates for ice at 30C.
of sea ice?"
7



 Previous Page
Previous Page
