trix with inclusions of brine, air and perhaps solid
coefficients of ice and brine (Grenfell 1983). Ab-
salts. Since these inclusions have different indices
sorption by air is assumed to be negligible.
of refraction than the surrounding ice, they scat-
Equation 4 provides a simple means of gener-
ter light. The larger the difference in index of
ating an absorption coefficient for sea ice from
refraction between the inclusion and the ice, the
physically determinable quantities and known
stronger the scattering. Sea ice has an abundance
values of ice and brine absorption coefficients.
of brine pockets and air bubbles and therefore is
Unfortunately, in nature, sea ice is often more
a highly scattering medium. In certain cases, par-
than a combination of ice, brine and air. For ex-
ticulates, sediment, and ice biota contribute to
ample, particulates, sediments, ice biota and dis-
scattering, but air bubbles and brine pockets are
solved organics can be present. If these impuri-
the primary scatterers in sea ice and are the focus
ties are present in sufficient quantity, then their
of this discussion.
absorptive properties must also be considered. In
Scattering results from differences in the real
general these impurities are strongly absorbing
indices of refraction (n) between ice (n ~ 1.31) and
and weakly scattering. Absorption coefficients for
the inclusions. With a greater difference in index
sediments and ice biota vary depending on their
of refraction, air bubbles (n ~ 1.0) are more strong-
composition. Examples of absorption coefficients
ly scattering than brine pockets. The real part of
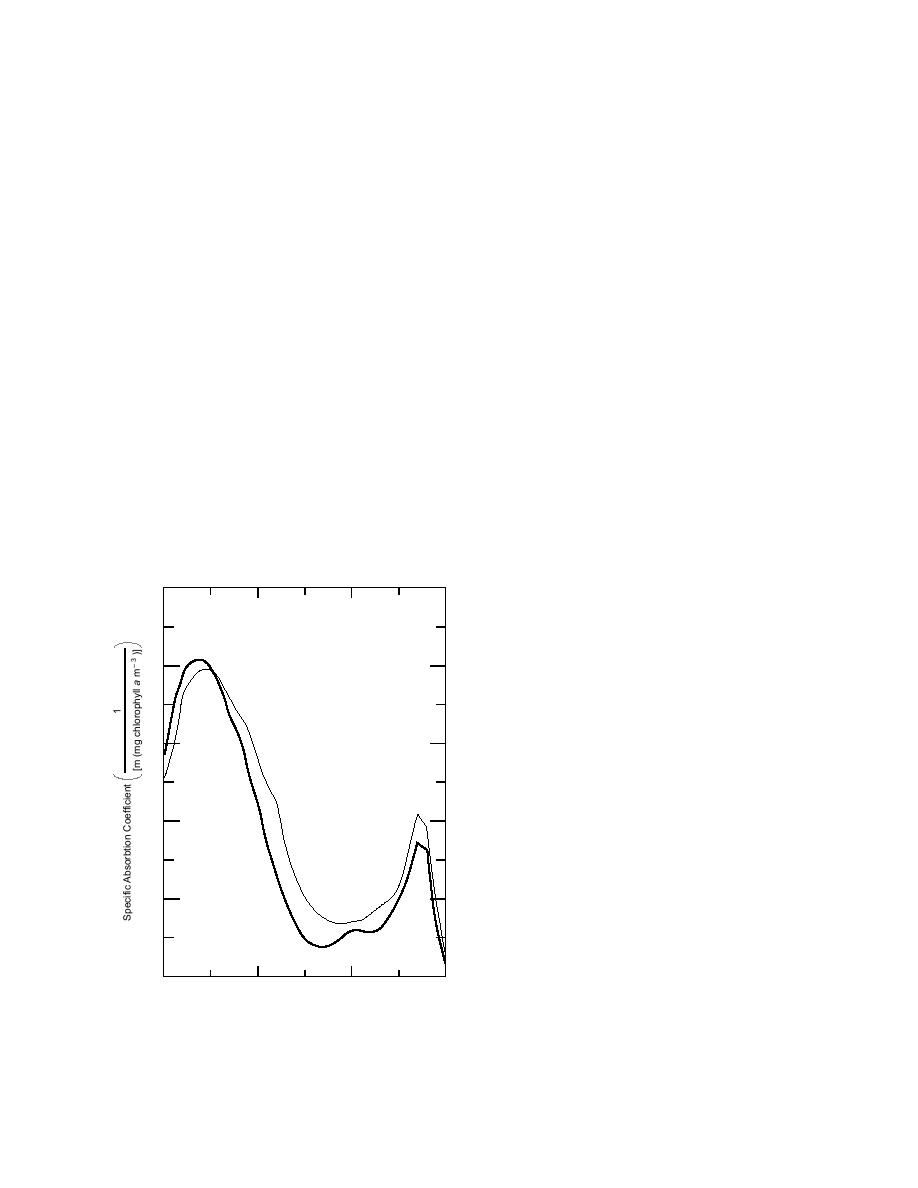
for ice biota (Arrigo et al. 1991) are shown in
the index of refraction for brine depends on tem-
Figure 6. The spectral shapes of these absorption
perature, increasing from 1.34 at 2C to 1.40 at
coefficients are quite different than those of ice or
32C (Maykut and Light 1995). If the ice is cold
brine. If sediment or ice biota are present in suffi-
enough that solid salts form, scattering increases
cient quantity, they should be explicitly treated in
the theoretical formulation by modifying eq 4.
significantly, since these salts are very effective
scatterers (Perovich and Grenfell 1981). The scat-
tering coefficient depends not only on the amount
Scattering
of brine and air, but on how it is distributed. This
Sea ice is not a monolithic slab of pure ice. It
complicates matters since the readily determined
has an intricate structure consisting of an ice ma-
brine and air volumes are not sufficient to define
scattering. The more difficult to obtain size distri-
bution of the inclusions is also needed. More in-
3
10 x 10
clusions in the ice results in more scattering and
consequently a larger scattering coefficient. Scat-
tering coefficients in sea ice are large, with values
typically greater than 10 m1 for warm ice and
8
greater than 200 m1 for ice with abundant air
bubbles or ice colder than 24C with precipi-
tated hydrohalite present (Perovich and Grenfell
1982).
6
Scattering is defined by two parameters: the
Congelation Ice
Community
scattering coefficient and the phase function. The
scattering coefficient (σ) is analogous to the ab-
sorption coefficient and is a measure of the
Platelet Ice
Community
amount of scattering per unit length. The phase
4
function [p(,′,φ, φ′)] describes the angular de-
pendence of scattering and usually is normalized
so that its integral over the full range of and φ is
equal to one.
2
Because scattering depends on the intricate and
highly variable microstructure of sea ice, it is not
possible to formulate a simple, all-encompassing
equation to define the scattering coefficient and
0
the phase function, as we could for the absorp-
400
500
600
700
Wavelength (nm)
tion coefficient. Complicating matters even fur-
Figure 6. Absorption coefficients of biota found in
ther is the fact that in a highly scattering medium
congelation ice and frazil ice (from Arrigo et al. 1991).
such as sea ice, scattering coefficients and phase
6



 Previous Page
Previous Page
