and contaminants, and that it is a material that
as the equation of radiative transfer for a plane
exists at its salinity-determined melting point.
parallel medium (Chandrasekhar 1960):
Therefore, changes in temperature result in
dI (τ, , φ, λ)
= I (τ, , φ, λ) - S (τ, , φ, λ) (2)
changes in its physical properties and structure.
-
dτ
One of the goals of this tutorial is to illustrate, at
least qualitatively, how changes in the ice physi-
where I = the radiance
cal properties are related to changes in optical
= the cosine of the zenith angle θ
properties. To accomplish this, we must first ex-
φ = the azimuth angle.
amine the theoretical underpinnings of radiative
transfer in sea ice.
Scattering is included in the S term, which is re-
ferred to as the source function. τ is the nondi-
mensional optical depth and is defined as
THEORY
[
]
τ (λ) = k (λ) + σ (λ) z
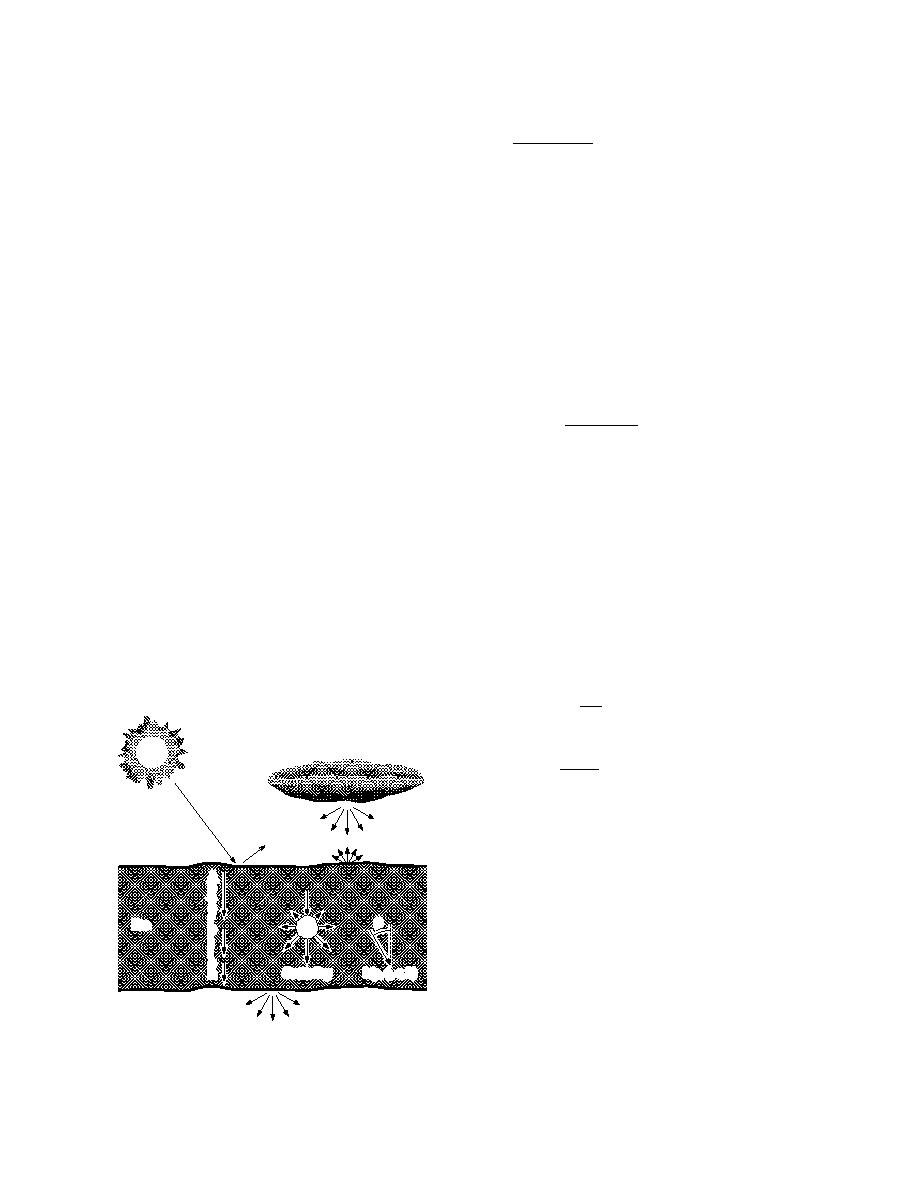
The interaction of solar radiation with sea ice
where k is the absorption coefficient, σ is the scat-
is illustrated schematically in Figure 4. The inci-
dent radiation field consists of a direct beam com-
tering coefficient, and z is the physical depth. The
ponent from the sun and a diffuse component
single scattering albedo
from the sky and clouds. If it is completely cloudy
σ (λ)
ϖ0 (λ) =
and the solar disk is not visible, the incident ra-
k (λ) + σ (λ)
diation field is considered to be diffuse. Depend-
ing on sky and surface conditions some portion
gives the fractional loss due to scattering (Chand-
of the incident radiation is specularly reflected
rasekhar 1960, Mobley 1994). ϖ0 ranges from 0 for
from the surface. A portion of the incident radia-
a purely absorbing medium to 1 for a purely scat-
tion is reflected from the ice, a portion absorbed
tering medium. A plane parallel medium is hori-
in the ice, and a portion transmitted through the
zontally homogeneous, but can have vertical
ice. As we shall see, the relative sizes of these
variations.
portions are dependent on the physical proper-
The compact form of eq 2 belies its true com-
ties of the ice and on the wavelength of the light.
plexity. This complexity becomes evident if there
At optical wavelengths, radiative transfer in
is scattering in the medium (ϖ0 > 0) and the source
sea ice is governed by two processes: absorption
function is expressed in detail. For a plane-paral-
and scattering. As a ray of light passes through
lel medium with a direct incident beam, the source
sea ice, some of the light is absorbed by the ice
function is expressed as
and some of it is scattered from the beam in dif-
1 2π
ferent directions. This is expressed more formally
ϖ
S (τ, , φ, λ) = 0
∫ ∫ p (, ′, φ, φ′) I (τ, , φ, λ)
4π
-1 0
E0 (λ)
p (, ′, φ, φ′) e ( ) 0 ,
-τ λ /
d′ dφ -
4
where p(,′,φ,φ′) is the phase function and E0 is
Direct
IDiffuse
the radiance of the direct beam component of the
Solar
ncident
R pecular
S
incident radiation field. With scattering included,
Beam
eflection
R Diffuse
Air
eq 2 is an integro-differential equation and is not
eflectance
readily amenable to solution. However, while it
b
A
s
is difficult to solve the equation, it is still straight-
o
r
forward to understand qualitatively. The double
p
Ice
integral term is used for diffuse radiative pro-
t
i
cesses only and represents scattering of the radi-
o
ance field I(τ,′,φ′,λ) from different directions into
n
I (, φ, τ, λ)
Scattering
the direction of the solution (,θ). How much of
this light is scattered from one direction to an-
other is defined by the phase function p(,′,φ,φ′).
Transmittance
Ocean
Figure 4. Schematic of radiative transfer in sea ice.
The phase function is normalized so that its in-
4



 Previous Page
Previous Page
