Figure 4. Rectangular enclosure configuration of Ghaddar

Figure 3. Cross section of a concentric pipe conduit

Figure 5. Experimental configuration of Stewart and Verhulst

CR99_07
Page Navigation
8

hexagonal cylinders inside a circular cylinder. He

found that the Nu should be based on gap width

while Ra should be based on the radius of the

internal cylinder. This approach indirectly

includes the aspect ratio used by other investi-

gators (e.g., eq 24).

Powe and Warrington (1983) and Warrington

and Powe (1985) investigated cylinders and

spheres mounted in spherical or cubical enclo-

sures. Although their experimental correlations

are probably not appropriate to this study, some

of their observations are of interest. They used

parameter L/rs as a multiplier to the Ra number

in correlations similar to those above, where L is

Diameter

0.25 in.

the gap width and rs is the hypothetical spheri-

cal radius based on volume. This parameter is

used to account for the observation that, as the

interior body becomes smaller, the natural con-

vection phenomena can be divided into three

regimes. These regimes are (1) infinite atmo-

sphere solution for large L/rs, (2) enclosure solu-

tions for moderate L/rs, and (3) conduction solu-

1.86 in.

3.72 in.

tions for small L/rs. Additionally, Warrington and

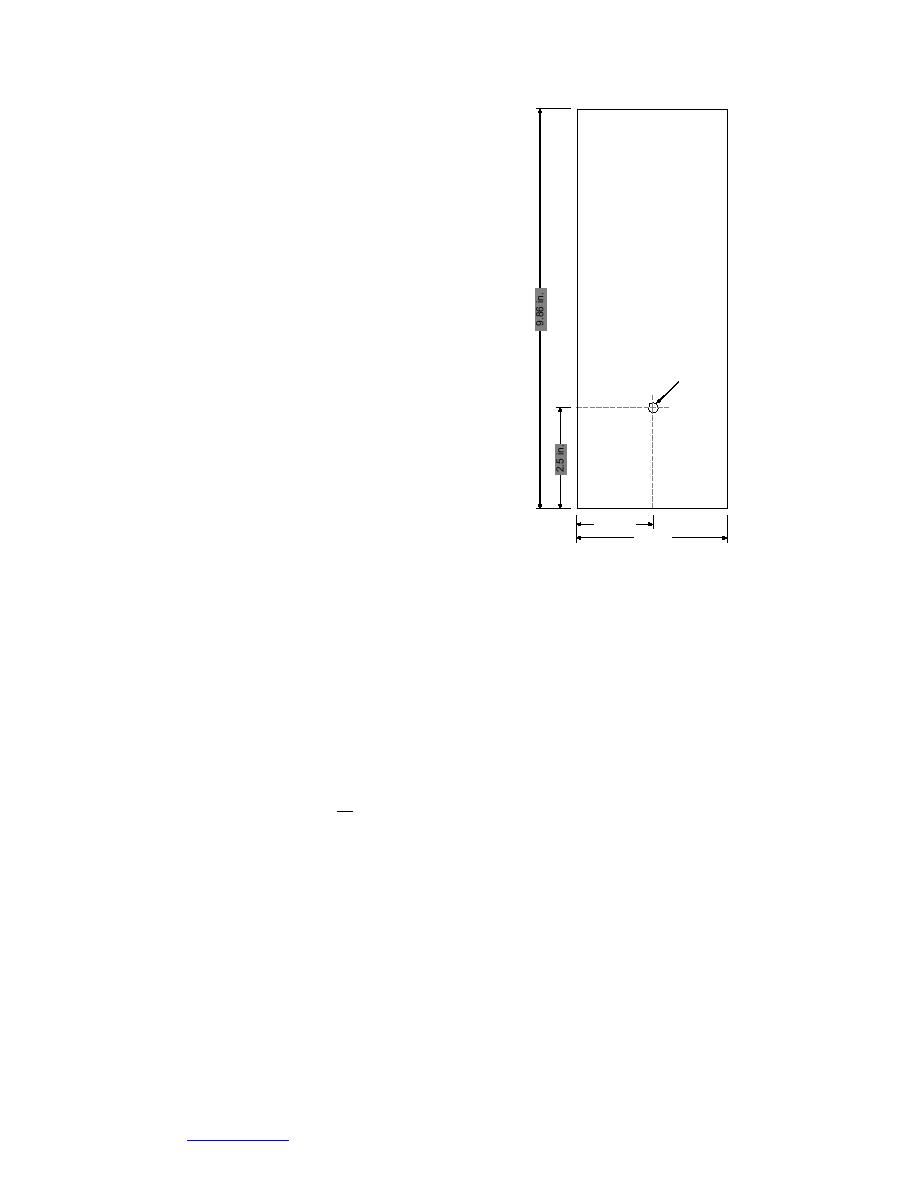
Figure 4. Rectangular enclosure

Powe (1985) determined that for nonisothermal

internal bodies, analyses using the average body configuration of Ghaddar (1992).

temperature compared well with results from iso-

thermal internal bodies.

Ghaddar (1992) conducted a numerical study of a uniformly heated (constant

heat flux) cylinder in an enclosure as shown in Figure 4. Note that the pipe is not

centered vertically, but is in the lower portion of the enclosure. She used a con-

stant wall temperature of 59F, and varied the heat flux into the cylinder; a mean

cylinder temperature was used to calculate the Rayleigh and Nusselt numbers. Her

numerical model did not include radiation. The heat transfer correlations devel-

oped were

0.207



 L 

NuL = 1.81 RaL   

(40)



 rp  





Nub = 0.604Rab.2083

(41)

where L is the hypothetical gap width, rp is the pipe radius, and b is the distance

traveled by the boundary layer on the pipe (half the pipe circumference). The

hypothetical gap width is defined as the difference between the effective radius of

a cylinder that has a circumference equal to the perimeter of the noncircular

enclosure and the radius of the interior pipe. Equation 40 becomes eq 42 after

inserting Ghaddar's test conditions into the L/rp term:

NuL = 3.756Ra 0.207 .

(42)

Go to Contents

Index

Privacy Statement
Press Release
Contact