channels to convey ice and water, or
whether jams usually occur because of
local channel irregularities (e.g., allu-
vial bars, flow features, channel con-
trol structures).
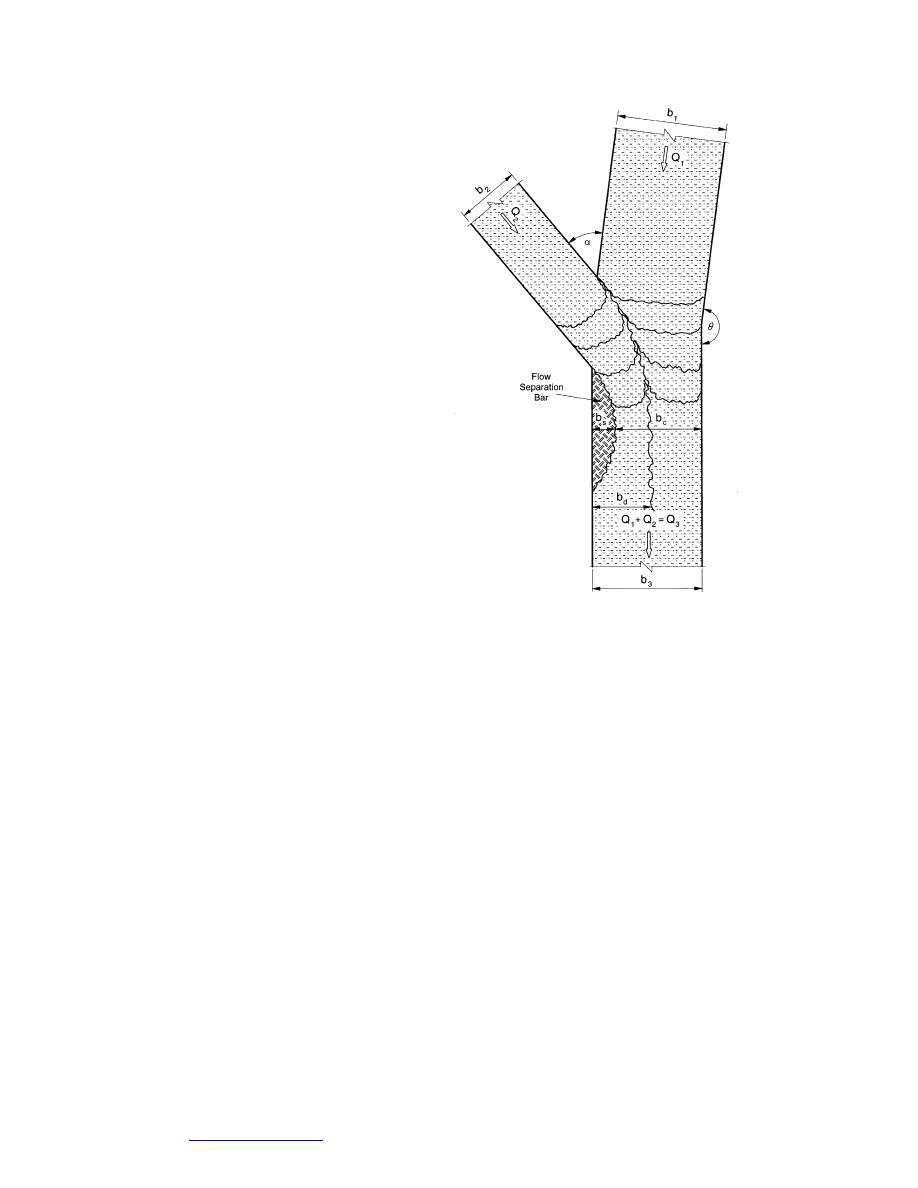
Ice drift through a confluence
Figure 8 indicates the variables asso-
ciated with water and ice discharge
through a confluence of two fixed-bed
channels of rectangular cross section.
The same size of ice piece is taken to be
moving through both channels. The
confluent inflow channels are desig-
nated with subscripts 1 and 2. The con-
fluence outflow channel is designated
with subscript 3. Variables at the most
constricted section of the confluence,
where the separation zone has maxi-
mum width, are designated with sub-
script c.
The discharge Q, unit discharge q, or
a representative velocity V of flow in
one of the channels shown in Figure 8
can be described using the variables Y,
b, S, and k, e.g., by means of the Darcy- Figure 9. Schematic of ice layers moving
Weisbach equation for flow resistance. through a confluence (subcategory 2b).
The terms are defined in Figure 8. Note
that, in this discussion, the variables Q, q, or V can be used (with b, Y, and k) in-
stead of channel slope, S. The present analysis uses Q, as it gives more meaningful
parameters for describing confluent flows than do q, V, or S. The fluid properties
of concern are kinematic viscosity ν, density ρ, and surface tension strength σ. The
ice pieces, taken to be of uniform size, are describable using a characteristic plan
pieces and with the channel banks . The flow is driven by specific weight, γ = ρg,
with g = gravity acceleration. The discharge of free-drifting ice pieces moving at
nearly the surface water velocity in a single channel can be described in terms of
areal concentration C, and ice discharge, G ≈ C(hb) (Q/bY) = C(h/Y)Q.
A total of 14 variables are needed to describe the discharge of free-drifting ice in
a channel. To describe ice discharge in two channels, which differ only in geome-
try and discharges of water and ice, the number of variables increases to 21; added
are Q, Y, b, k, C, D, and h for the second channel. The material properties of water
and ice are taken to be the same for all channels. To describe the merging of ice
flow from two channels confluent into a single outflow channel, additional vari-
ables are needed to describe the orientation of the outflow channel relative to the
confluent channels, α and θ, and the hydraulic characteristics of the outflow chan-
nel (Q3, b3, Y3, and k3). The total number of variables is now 27.
For the simple case of no ice jamming, continuity of water, and ice discharges
through the confluence without jam formation, the following equations are
18
Go to contents page




 Previous Page
Previous Page
