given below. This approximate method requires that the maximum width of the
flow separation zone be first estimated, however.
Extent of flow separation zone
Several studies have investigated flow separation at a confluence of rectangular
channels. Their results are useful for estimating the likely contraction of the flow
area within a confluence. In addition, the size of the separation zone approximately
coincides with the size of the bar found in confluences of concordant channels.
Laboratory experiments, conducted using rectangular channels, led Gurram et
al. (1997) to the following semianalytical equation for the maximum width of the
separation zone:
1/2
Q
2
α
bs 1
2
= Fd - + 0.45 2
o
(4)
90
b3 2
3
Q3
where bs = the width of the separation zone,
b3 = the downstream width of the main branch,
Fd = the tailwater Froude number,
Q2/Q3 = the discharge ratio between the lateral to the downstream discharges,
α = the apex angle of the confluence.
Gurram et al. (1997) developed further equations for aspects of confluent flow,
including the pressure force on the lateral sidewalls, the ratio of flow depths in the
junction point, the momentum correction coefficient, and the lateral momentum
contribution. They showed that these flow variables depend primarily on the dis-
charge ratio, the tailwater Froude numbers, and the confluence angle.
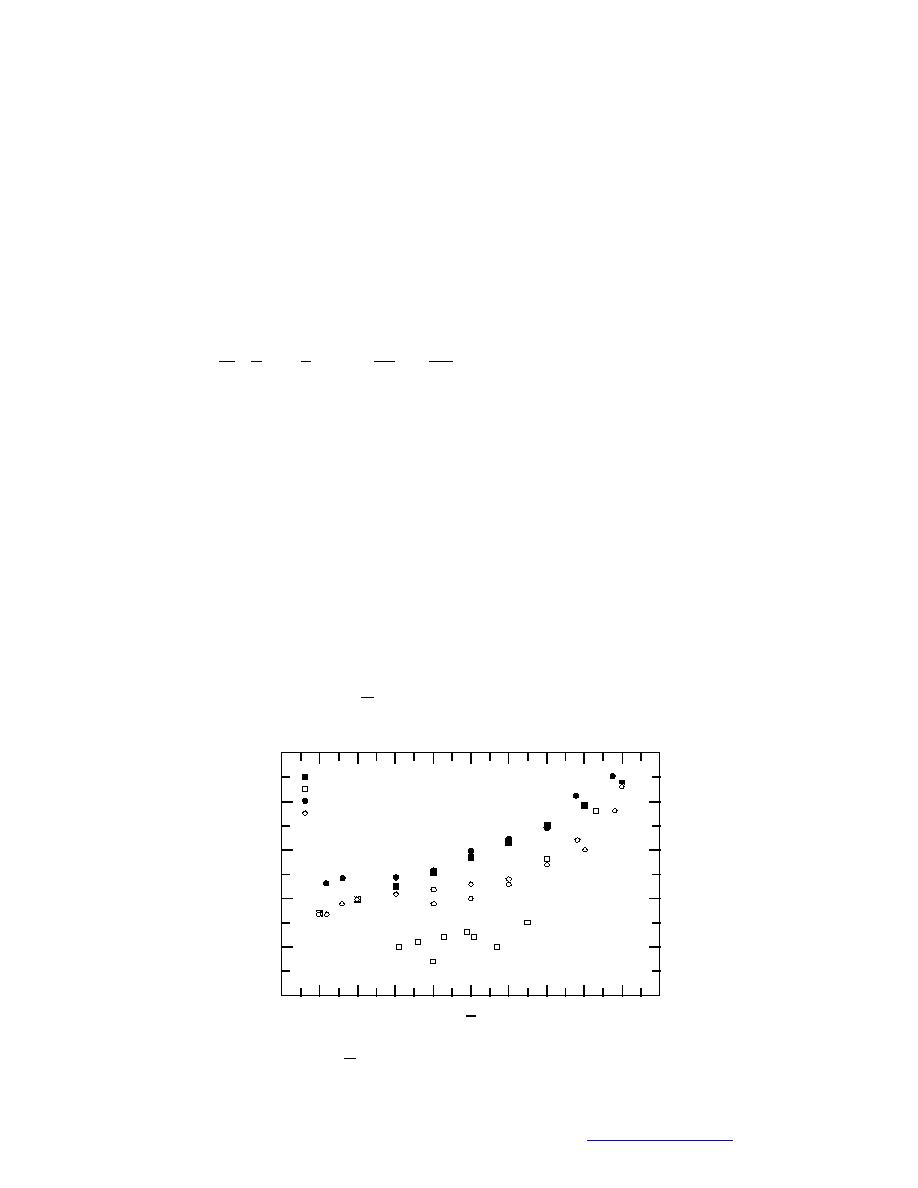
Hsu et al. (1998) analytically and experimentally investigated flow in the con-
fluence of two equally wide, rectangular channels oriented 90 to each other. Their
work resulted in a set of somewhat sketchy curves for estimating the maximum
width of the separation zone, as shown in Figure 6. In that figure, contraction
coefficient = bc/b3, and Q = Q2 / Q3 .
1.0
Hager, 1987 (predicted)
Best & Reid, 1984 (measured)
0.9
Present Study (predicted)
Present Study (measured)
0.8
0.7
0.6
0.5
0.0
1.0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
Q
Figure 6. Contraction coefficient at the maximum confluence constric-
tion; = bc/b3, Q = Q2/Q3. (After Hsu et al. 1998.)
13
Back to contents page




 Previous Page
Previous Page
