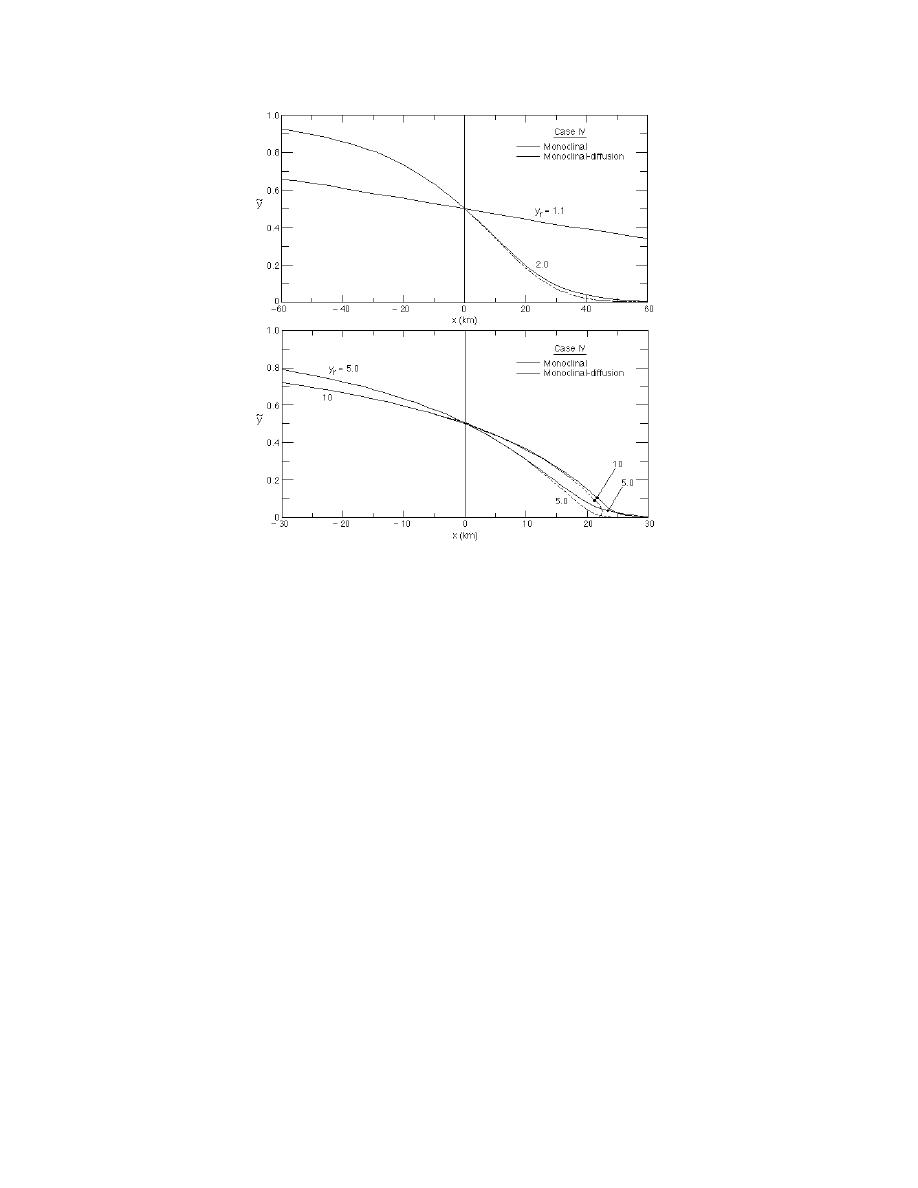
Figure 11. Case IV monoclinal and monoclinaldiffusion profiles at
two distance scales for depth ratios ranging between 1.1 and 10.
similar to case III with distance scales substantially increased. At yr = 2 the profiles begin to
separate at a dimensionless depth of about 0.3, and an overrun of the leading edge occurs at
yr = 10 up to a dimensionless depth of 0.03. Case V, presented in Figure 12, is qualitatively
similar to cases I and II except that the largest diffusion coefficient produces the longest pro-
files of all the cases.
General results from these comparisons are that monoclinal and monoclinal-diffusion
profiles agree for all values of yr with F0 ≤ 0.2, and that profile length increases with η or D.
At small F0 the depth ratio needed to produce a shock is large, and the shock height and
overrun distance of the leading edge are small. These results agree with the Lighthill and
Whitham (1955) contention that dynamic waves are subordinated at "well subcritical"
Froude numbers. As F0 increases the monoclinal waves differ over a larger portion of the
profile, shocks occur at smaller depth ratios and their dimensionless amplitudes increase,
and for a given η the profile length decreases. General dimensionless monoclinaldiffusion
profiles for each depth ratio are given in Figure 13 as a function of x , and include the profiles
~
of all cases as indicated by eq 35. Similar dimensionless monoclinal profile plots in Figure 14
are almost as well-behaved, but differences near the leading edge occur for each yr due to
their F0 dependence.
Steady flow rating curves relate river stage or mean depth at a given location to a unique
discharge. The governing equation for linear waves holds with either v or y as the depen-
dent variable, indicating a fixed steady flow rating. In unsteady flow the discharge relating
to a given stage generally varies from that for steady flow, depending on the rate of rise or
fall of the hydrograph. We will develop and compare dimensionless monoclinal wave and
steady flow ratings. Using eq 26, an equation for the monoclinal wave unit discharge can be
written in terms of depth and depth ratio as
18



 Previous Page
Previous Page
