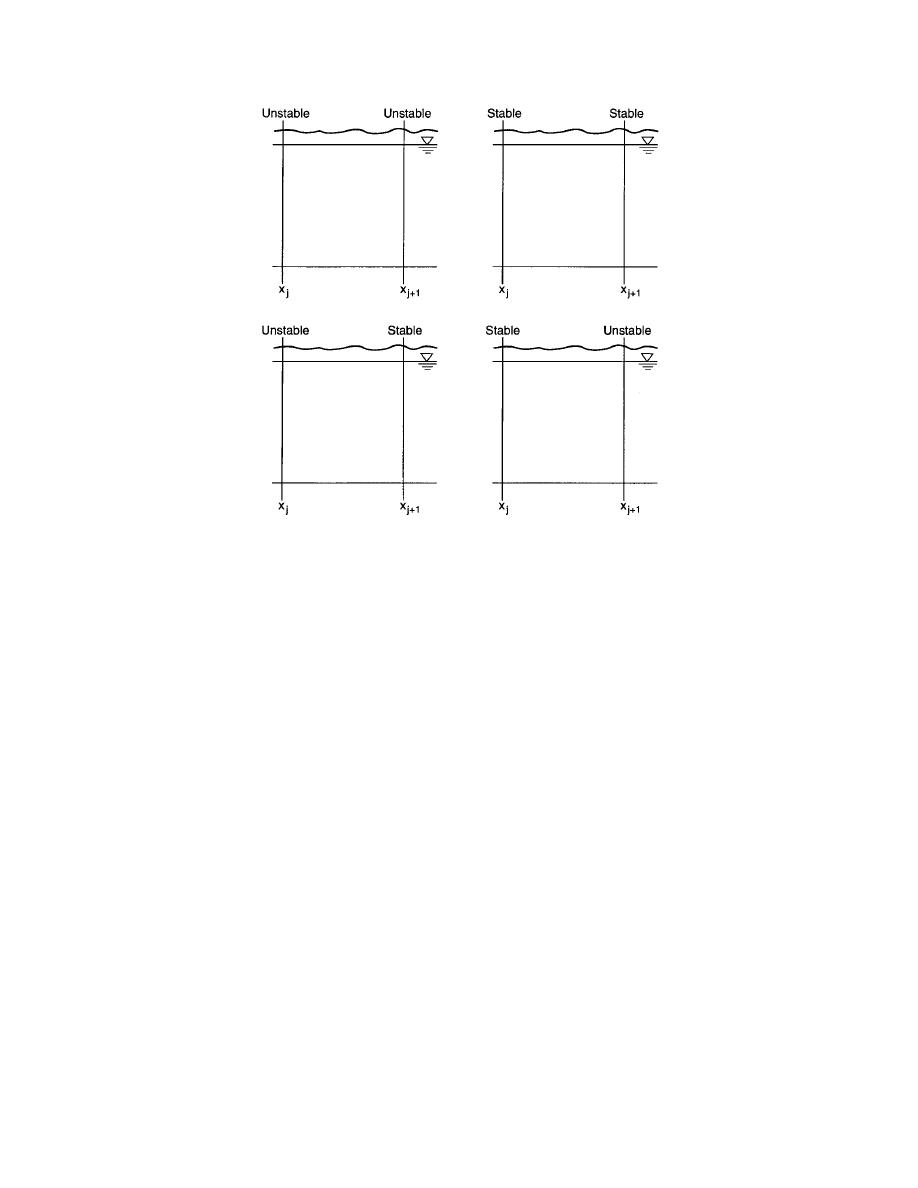
Figure 32. Conditions of ice jam stability for a computational reach.
Three modes of solution of the system of equations are presented below. The
fully coupled mode comprises the simultaneous solution of all four dependent
variables using the full equations and Newton-Raphson iteration technique pre-
sented above. The uncoupled or loosely coupled mode solves the water equations
and ice equations separately and sequentially, as is done in the moving ice model
of Tsai et al. (1988). The static-unsteady thickness mode first solves the water equa-
tions, then a modified version of the conservation of momentum equation not
including the ice-momentum component. This latter procedure is comparable to
the procedure used in stationary jam formulations.
Fully coupled solution
The fully coupled mode of solution uses the full equations of mass and momen-
tum conservation for the water and ice with the simplifications mentioned above
for sections and reaches that are determined to be stable. The four dependent vari-
ables are solved simultaneously using the Newton-Raphson iteration scheme men-
tioned above. The coefficient matrix, as depicted in Figure 31, is solved by decom-
positionback-substitution using banded-matrix manipulation techniques. The
coefficient matrix is a banded symmetrical matrix with five bands above and five
below the main diagonal. Four equations for each reach relate the 4N unknowns,
where N is the number of cross sections. Two boundary condition equations at the
upstream end and two at the downstream end are required to close the system. The
upstream boundary conditions are typically a water discharge relation (e.g., speci-
fied discharge) and an ice thickness relation (such as static equilibrium or specified
thickness). The downstream boundary conditions are typically a specified depth
relation (under ice) and an ice velocity relation.
51




 Previous Page
Previous Page
