Figure 34. Block diagram for the loosely coupled solution scheme

Loosely coupled solution

Static-unsteady thickness solution

CR97_07
Page Navigation
53

Input Initial Conditions

Water/Time Step

Ice Stability Check

Water Equations

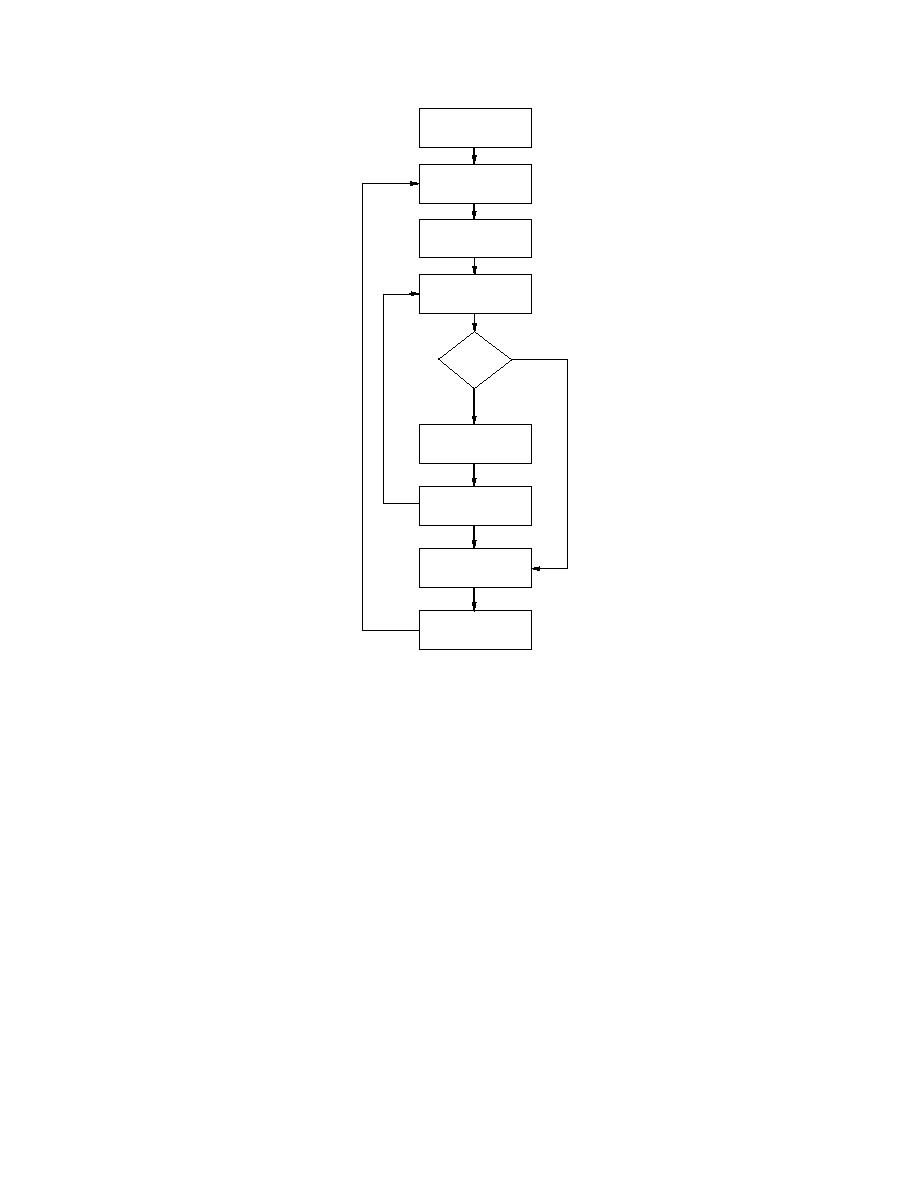
Figure 34. Block diagram for the

loosely coupled solution scheme.

above and two below the main diagonal. Two equations for each reach relate the

2N (water or ice) unknowns. A single boundary condition at the upstream and the

downstream ends is required to close the system.

The block diagram for the loosely coupled solution scheme is presented in Fig-

ure 34. The initial conditions are read, the timer incremented, and boundary condi-

tions for the new time step obtained. The ice variable solution can have a different

time step than the water variable solution and is specified as an even fraction of the

water time step. This procedure is needed because the ice variables can change

faster than the water variables, especially when moving ice stops and thickens. The

ice cover stability is checked, the ice variable coefficient matrix is computed and

solved, tolerances are checked, and the ice variables are reset for the next ice time

step. If the entire ice cover is found stable, the ice variables are simply reset and the

ice time step incremented. Following the correct number of ice time step calcula-

tions, the water coefficient matrix is computed and solved, tolerances checked, and

the water variables reset. This solution mode is included as a comparison to the

fully coupled mode because there are currently no existing formulations that are

Western Governors University

Privacy Statement
Press Release
Contact

Integrated Publishing, Inc. - A (SDVOSB) Service Disabled Veteran Owned Small Business