Open Files
Input Initial Conditions
Increment
Time Step
Input
New Boundary
Conditions
Iterate
Ice Stability Check
All
Reaches
Yes
Stable
No
Solve Full System
of Equations
Solve Water
Reset Variables
Equations Only
Write Output
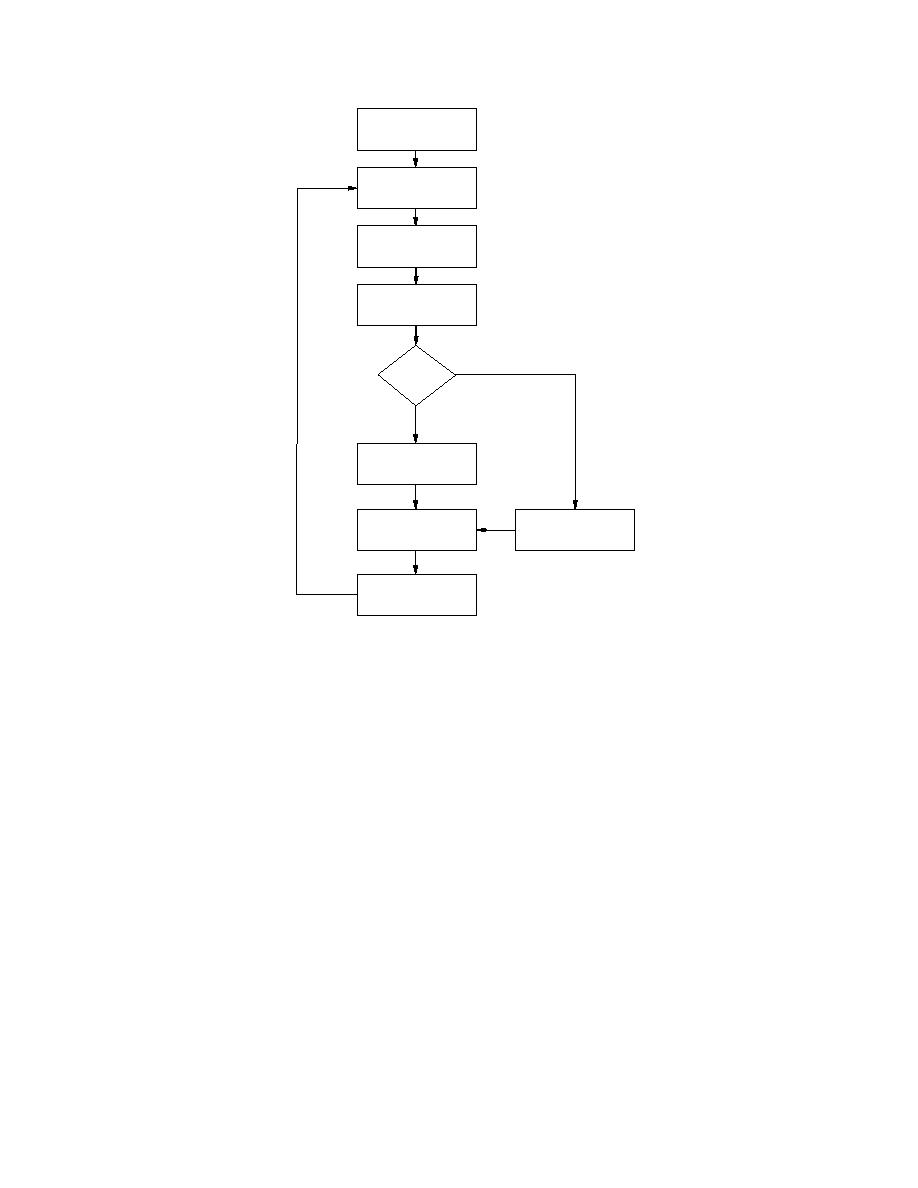
Figure 33. Block diagram for the fully coupled solution scheme.
The block diagram for the fully coupled solution scheme is presented in Figure
33. The initial conditions are read and the timer incremented. Boundary conditions
for the new time step are read and local jam stability checked. The coefficient
matrix is then computed and solved, tolerances are checked, and variables are reset
for the next time step. For special cases when the entire ice cover is deemed stable,
the solution reverts to only the water variables, as the ice variables will remain
constant. In this case, an abbreviated coefficient matrix is developed and solved
that contains only two equations per reach and the two water boundary condition
equations (water discharge upstream and water depth downstream). This abbrevi-
ated matrix is a banded symmetrical matrix with two bands above and two below
the main diagonal. The reversion to the abbreviated coefficient matrix reduces com-
putation time.
Loosely coupled solution
The loosely coupled mode of solution also uses the full equations of mass and
momentum conservation for the water and ice, including the simplifications for
sections and reaches that are determined to be stable. However, in this mode, the
water variables are solved separately and sequentially from the ice variables. Both
solutions are by the Newton-Raphson iteration scheme presented above. The coef-
ficient matrix for each solution is a banded symmetrical matrix with two bands
52



 Previous Page
Previous Page
